Theory and simulations

Ferroelectric materials, films and heterostructures
The ferroelectrics host spontaneous ferroelectric polarization, which can be switched between several equivalent directions. As the polarization is usually strongly coupled to mechanical deformation, the switchichg can be achieved by either electic field or by application of pressure...
The switching of polarization is a key ingredient in their large dielectric and piezoelectric response, which find utility in vast number of applications related to actuation and sensing. The existence of several equivalent polarization states leads to appearance of the ferroelectric domain structure, a pattern formed by regions of approximately homogeneous polarization state and interfaces between them (see figure). The switching depends strongly on properties of the interfaces, in particular on their ability to move.
Ferroelectric order only exists below the Currie temperature, and the material can undergo several transitions between diffent phases upon further cooling, with the electromechanical properties usually strongly elevated in the vicinity of transitions. Another way of achieving elevated properties is tuning chemical composition in solid solutions of multiple ferroelectrics, which might give rise to a region of morphotropic phase boundary (MPB), where two symmetry variants of the material are very close to each other. The MPB materials exhibit better stability of properties in devices which operate in a wide temperature range. Finally, the materials can be brought towards phase transition using suitable electro/mechanical conditions, such as hydrostatic pressure or epitaxial strain in thin films.
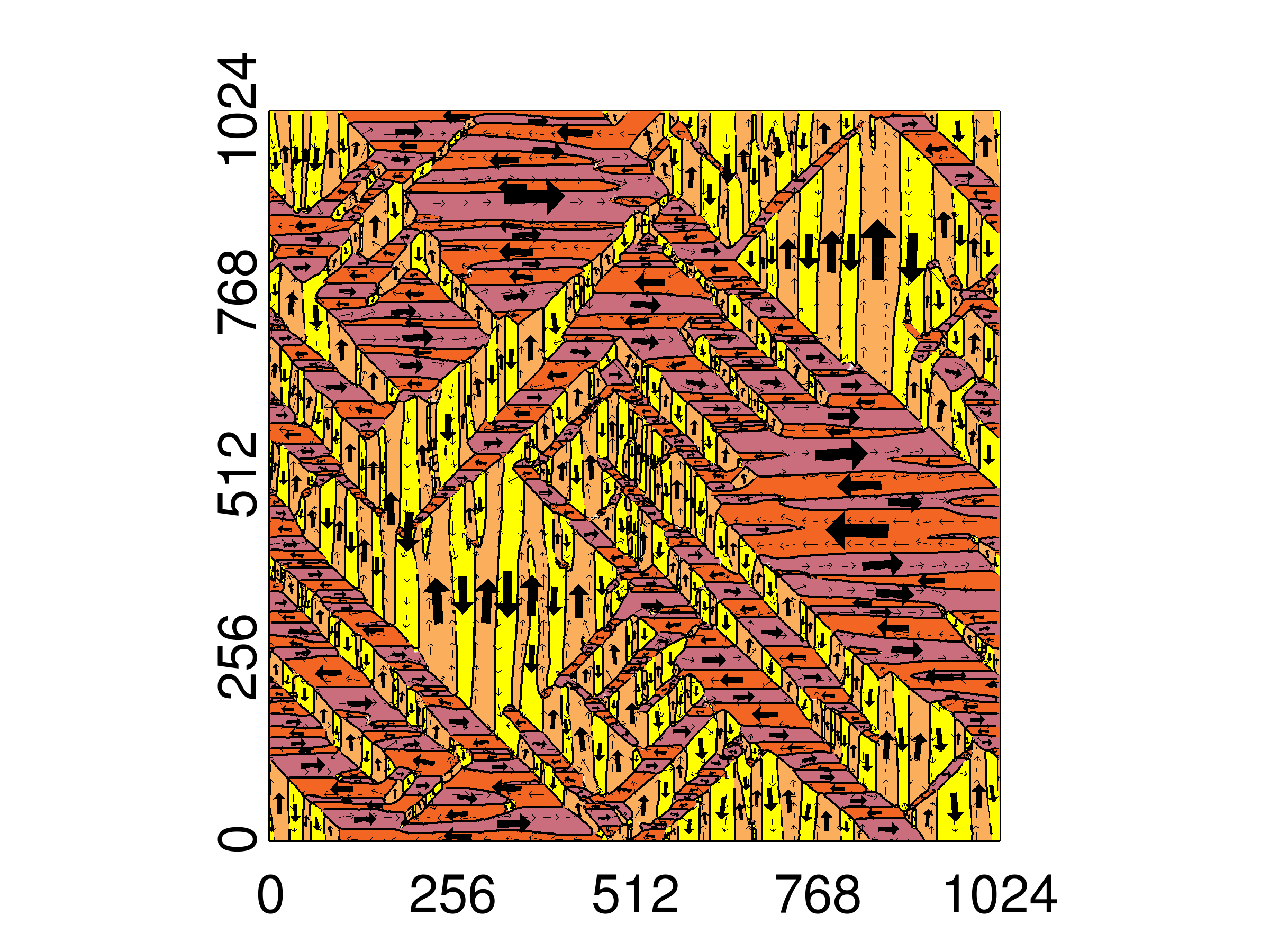
Figure: Domains structure in the tetragonal phase of BaTiO3 simulated using phase-field model in the programme ferrodo. Different colors mark domains with distinct orientations of spontaneous polarization.
Phase transitions, presence of complicated domain structures, domain interfaces with properties depending on local (defect) chemistry makes the materials challenging experimentally as well as theoretically, and yet, understanding them is a crucial prerequisite for full exploitation of their exceptional properties.
In a close collaboration with experimentalists we investigate structural properties of ferroelectrics, target their dynamics, study domain structures and their impact on material properties, and even consider properties of domain-engineered patterns. Our tools range from first-principles calculations of intrinsic material properties, through atomic-level empirical-potential-based simulations up the phenomenological Landau-Ginzburg-Devonshire (LGD) theory for ferroelectrics. We have strong background in application of the LGD theory to investigate properties and details of the domain interfaces using analytical calculations. To deal with complex domain structures we developed and maintain a computer code ferrodo, which allows for time-dependent phase-field simulation of ferroelectric-domain-structure evolution within the framework of the GLD model. Ourselves, we develop parametrizations of the GLD models for ferroelectrics of interest.
We are also active in the field of epitaxially grown structures. These are e.g. thin films as well heterostructures, which are composed of layers of multiple different materials forming periodic superstructure. The strain mismatch between film and substrate or between layers of the superstructure profoundly changes properties of the ferroelectric part. Recent advances in techniques of epitaxy allowed for unprecendented precision of deposition with possibility to control number of atomic layers. This leads to emergence of self-assembled domain nanostructures, which are of strong interest of the scientific community, us notwithstanding.
(show less)

Modelling of mesoscopically heterogeneous systems (effective medium)
For decades, understanding of mesoscopically heterogeneous systems is of a great interest from fundamental as well as from practical perspectives, mainly because great deal of the functional materials for applications are currently produced in the form of ceramics and composites...
The word ‘mesoscopic’ points out to the size of inhomogeneities, which are all much larger than a typical interatomic distance. Consequently they can be often treated as composed of regions with homogeneous material (macroscopic) properties separated by thin boundaries. Depending on the concrete system the inhomogeneities are called grains (ceramics), clusters (composites), or microdomains (ferroics). The overall properties are not simple average of components’ properties, but are crucially impinged by electric charges or mechanical stresses induced at the boundaries. This can lead to a deterioration or also an improvement in the properties, depending on the target requirements. The micro-geometry can crucially tune the properties of the samples, e.g. the dielectric matrix with metal nearly percolated inclusions yields high-permittivity systems, highly appreciated in applications. For practice, the main goal is to achieve the ability to construct the composite of the required properties.

Figure: a) Realistic three-dimensional model of BaTiO3 ceramics, whith constructed mesh for calculations using finite element method. Clearly visible are pores between ferroelectric grains. b) For comparison, the experimental micrograph of the same material.
Therefore the main theoretical task concerns the relationship between the overall properties (dielectric, elastic, etc.), and the mesoscopic (regular or random) geometry and properties of the constituents. If the wavelength of the probing field is large in comparison with the dimension of inhomogeneities (the long-wavelength limit), the effective medium approaches are widely used, and leads to various mixing formulas describing the effective response (for example, a ‘classical’ Maxwell-Garnett relation). For two-component systems the exact analytic dependence of properties of the effective permittivity is studied using integral representation allowing separation of the micro-geometry and material properties, which turns important for interpretation of experimental data and construction of new models. Description of more complicated systems, such as those with multiple components is much more complicated and awaits for theoretical progress. The construction and analysis of the appropriate finite element models is a complementary method in study of the effective properties.
(show less)
Relaxors and disordered ferroelectrics
We devote a lot of effort to understand the nanoscale phenomena in chemically disordered dielectric materials. These materials exhibit exceptionally large piezoelectric and dielectric responses and are therefore utilized in vast number of devices...
However, due to their complexity at different scales, they are by far not well understood yet, which hinders the efforts to fully exploit their potential. We work in a close cooperation with experiment to shed light on mechanisms behind their performance.
Our tools are dominantly numerical large-scale molecular-dynamics simulations. The interactions between individual atoms are treated classically in order to allow for large and long-enough simulations, necessary for extraction of spatial and time correlations. The simulations allow us to extract the diffuse scattering paterns reflecting static chemical as well as dynamical/vibrational disorder, and compare them directly to experimental data. As the relevance of the obtained results strongly depend on the quality of parametrers characterizing the interatomic interactions, we built the comptetence of developing new and improving exiting models. Using carefully chosen models, the simulated and experimentally obtained results are remarkably similar, indicating that they capture well the physics of atomic interactions.

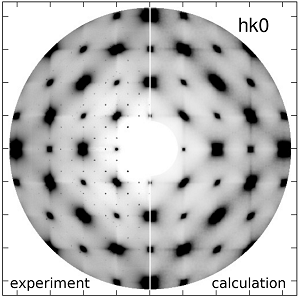
Figure: Diffuse scattering patterns on hk0 and hk0.5 reciprocal planes for cubic BaTiO3. Left side of each circle contains experimental data, calculated patterns are on the right. The patterns characterize a dynamical disorder present in this material in its paraelectric phase (the data were collected at 500 K, ~100 K above the transition to the ferroelectric phase).
SrxBa1-xNb2O6 (SBN) is one of the materials of interest. This solid solution has a tunable ferroelectric behaviour – it can be a 'normal' ferroelectric with a sharp phase transition at a certain temperature for small Strontium concentrations or a 'relaxor' material in which the dielectric permittivity has an anomaly in a broad temperature range which additionally depends on the frequency of the probing electric field. The relaxor behaviour is usually attributed to the existence of small polar clusters or nanodomains. These have been extensively studied by a combination of neutron scattering techniques and phenomenological modeling. An atomic-level combination of theory (using first-principles quantum-mechanical calculations) and a scattering-based analysis (neutron pair distribution function) yields a picture of two polarization sublattices influenced by the chemical disorder and a short-range nature of non-polar distortions. A raman scattering experiment in conjunction with an infra-red and THz spectroscopic methods, covering together a broad frequency range, also indicate on an existence of more then one polarization mechanism contributing to the complicated dielectric behaviour of the relaxor SBN.
Another chemically disordered material is the PbZr1-xTixO3 (PZT), which is one of the most used piezoelectric compounds with superior electromechanical properties at special composition ratio of Zr and Ti atoms (called morphotropic phase boundary region). The random distribution of these ions makes any analysis of experimental data notoriously difficult. However a purposely designed mathematical analysis of the Raman spectra based on their frequency derivatives was instrumental in unveiling a 'hidden' contributions to the recorded signal. This helped to clarify the nanoscale picture of this material in the interesting compositional range. A follow-up study, again using broad range of probing frequencies, showed how a mesoscale structural features – domain walls and grain boundaries – dominate the dielectric response at room temperature and below.
(show less)
Symmetry analysis of crystalline materials
The crucial role of symmetry considerations is well appreciated in contemporary physics, and it is extremely important in highly anisotropic crystalline materials ungergoing phase transitions, which we are generally interested in...
We therefore study various symmetry aspects of structural and magnetic phase transitions, Landau theory, order parameters, role of the time-reversal symmetry, symmetry breaking and spontaneous macroscopic properties, as well as symmetry of domain walls and other topological defects. From this list it is clear that our efforts typically, but not exclusively, apply to ferroic materials, which is the main theme of the Department of Dielectrics.
We serve the community via detailed investigating and publishing systematic general results and overviews. These include lists of all possible reductions of macroscopic crystallographic symmetry of crystals, related to the associated changes in the macroscopic property (available on – http://palata.fzu.cz/species/13x13axial), symmetry classification from the point of view of the octuplet of vector-like quantities, as well as participation in compilation of the International tables for crystallography.
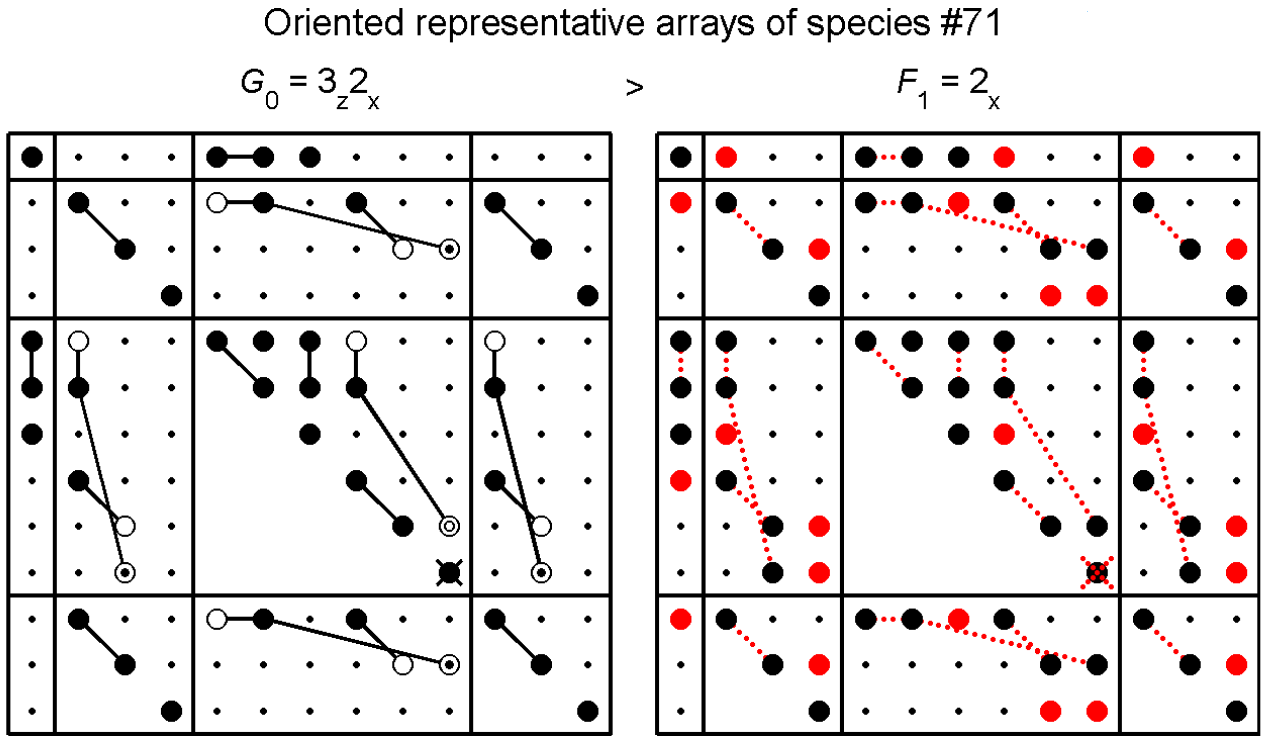
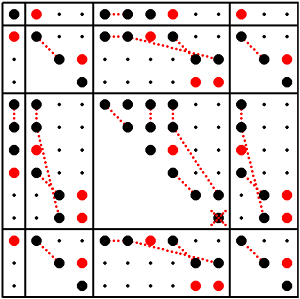
Figure: Matrices of material property tensors for a symmetry-breaking structural phase transition between two phases (characterized by different point-group symmetry), showing relations between tensor components of both phases and emergence of spontaneous components (red points).
(show less)
Quantum criticality and quantum phase transitions
Quantum physics governs the dynamics of particles at microscopic distances and very low temperatures. If the coherence between the particles extends to macroscopic distances, the laws of quantum mechanics affect the global behavior of solids and may manifest itself in macroscopic effects such as phase transitions.
Quantum critical behavior is realized and observed in systems with a strong interaction between the valence electrons of solids. Itinerant magnetism and superconductivity are the paradigm quantum macroscopic phenomena in strongly correlated electron systems.
However, despite of its imporatnce for potential applications, a comprehensive theory of quantum critical behavior comparable with that of classical criticality is still missing. Therefore, we use the technique of Green functions and Feynman diagrams to assess analytically the effects of strong electron interaction with the aim to describe quantum critical behavior in nanoscale as well as bulk materials.
Our approach is based on renormalization of the electron interaction balancing multiple scatterings of electrons with other electrons and holes. The ultimate objective is to develop a semi-analytic thermodynamically consistent theory of mean-field type of quantum critical behavior and quantum phase transitions, which would qualitatively correctly take into account both the local quantum dynamical and spatial fluctuations in thermodynamic as well as spectral functions of strongly correlated solids.
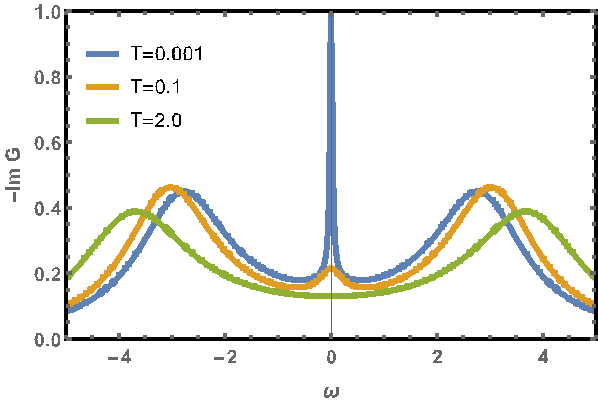
Figure: Typical temperature behavior of the spectral function of strongly correlated electron systems with no long-range order. The combined effect of strong electron repulsion and thermal fluctuations expel electrons from the Fermi energy to satellite Hubbard bands. Lowering the temperature enhances the quantum coherence and a narrow central quasiparticle peak starts to develop reflecting formation of local magnetic moments in metals while the Hubbard bands remains present. The energy unit is the effective bandwidth of the metal.
(show less)