Theory and simulations
Pyramidal charged domain walls in ferroelectric BiFeO3
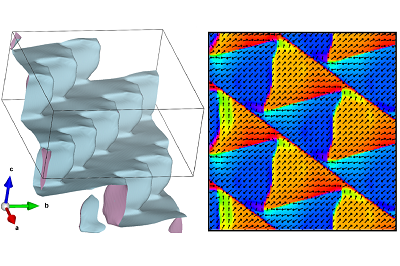
We uncover the physical origins of the enigmatic zigzag domain structure in the prototypical multiferroic material BiFeO3. Using phase-field simulations, we demonstrate that spatially-homogeneous defect charges result in domain structures that closely resemble those observed experimentally. The acquired understanding of the underlying physics of pyramidal-domain formation may enable the engineering of new materials with self-assembled domain structures. [Commun. Mater. 6, 161 (2025)].
We addressed a long-standing puzzle in ferroelectric research: the origin of unusual zigzag and pyramidal domain structures in the multiferroic material BiFeO3. These complex patterns had been observed experimentally for years, but their physical cause remained unclear. Using phase-field simulations within the Landau–Ginzburg–Devonshire framework, we demonstrated that they can naturally form when defect charges are distributed homogeneously in the crystal. The system compensates these charges by creating pyramid-like domains in which the polarization rotates to lower the overall energy. Our simulated patterns agree closely with transmission electron microscopy observations of BiFeO3 crystals from our colleagues at the University of Warwick, giving strong support to our model. Beyond solving a fundamental question, this insight has practical value. The pyramidal domains are highly regular and self-assembled with nanometer-scale periodicity, making them attractive for applications requiring precise ordering, such as optics or topological defect-based devices.
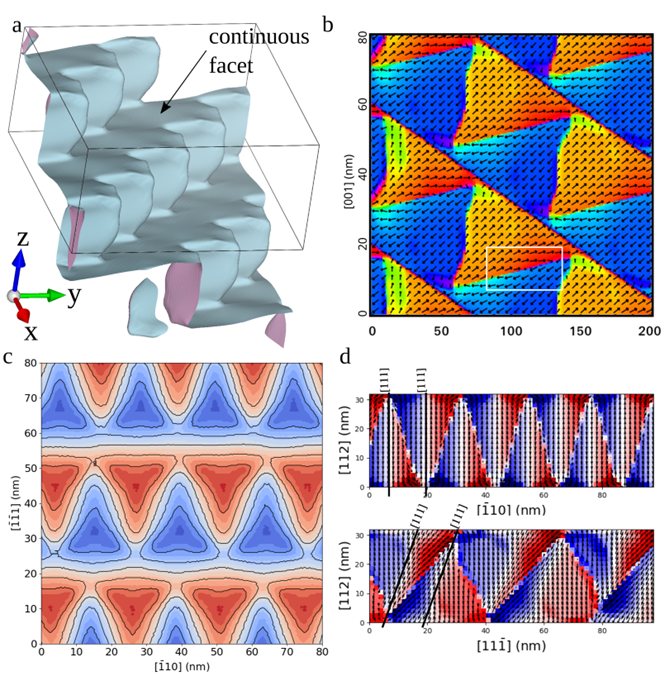
Phase-field simulations for a rhombohedral ferroelectric material:
a) 3D visualization of the wall surface.
b) Ferroelectric polarization visualized in the plane (-110).
c) Distance of the domain wall from the center of the charged layer measured along [111].
d) Deviation of the polarization from the pyramid’s axis.
Polarization is projected to two selected planes, color indicates polarization component perpendicular to [111] direction.
Red: positive, blue: negative, white: no deviation.
[1] P. Marton, M. Paściak, M. A. P. Gonçalves, O. Novák, J. Hlinka, R. Beanland, and M. Alexe, Pyramidal charged domain walls in ferroelectric BiFeO3, Commun. Mater. 6, 161 (2025).
(show less)
Antiskyrmions in ferroelectric barium titanate
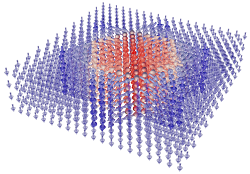
Our recent molecular dynamics computational study reveals that the bulk crystal of the archetypal ferroelectric perovskite BaTiO3 can host ferroelectric antiskyrmions at zero field. We show that the antiskyrmion has just 2-3 nm in diameter and that it carries a very exotic topological charge of minus two [Phys. Rev. Lett. 133, 066802 (2024)].
The prediction and experimental confirmation of magnetic skyrmions revolutionized the physics of nanoscale magnetism and opened new horizons for spintronics. In spite the inherently shorter and faster correlations of the electric polarization and challengingly smaller correlation lengths, the recent developments in electric skyrmionics follow these innovations. It is only 5 years since the first observation of a ferroelectric skyrmion in thin lead-strontium titanate superlattices [1].
The present molecular dynamics computational study [2)] reveals that the bulk crystal of the archetypal ferroelectric perovskite (barium titanate) can host peculiar 2-3 nm wide standalone polar columns stable till temperatures of several tens of Kelvins. They are spontaneously surrounded by a unique noncollinear polarization pattern (see figure) that has never been described before. We explained how and why this pattern is formed and stabilized. Since its invariant skyrmion topological charge is an integer with a sign opposite to that of the usual skyrmions, they named this soliton as ferroelectric antiskyrmion. They clarify that formation of antiskyrmions consists in breakdown of high-curvature 180-degree ferroelectric walls into triplets of lower-energy 71-degree walls. It is explained that this process is favored by a fortunate combination of the moderate anisotropy of the anharmonic electric susceptibility and the pronounced anisotropy of the polarization correlations in barium titanate crystals. These findings represent a clear milestone in the studies of topological defects in ferroelectrics.
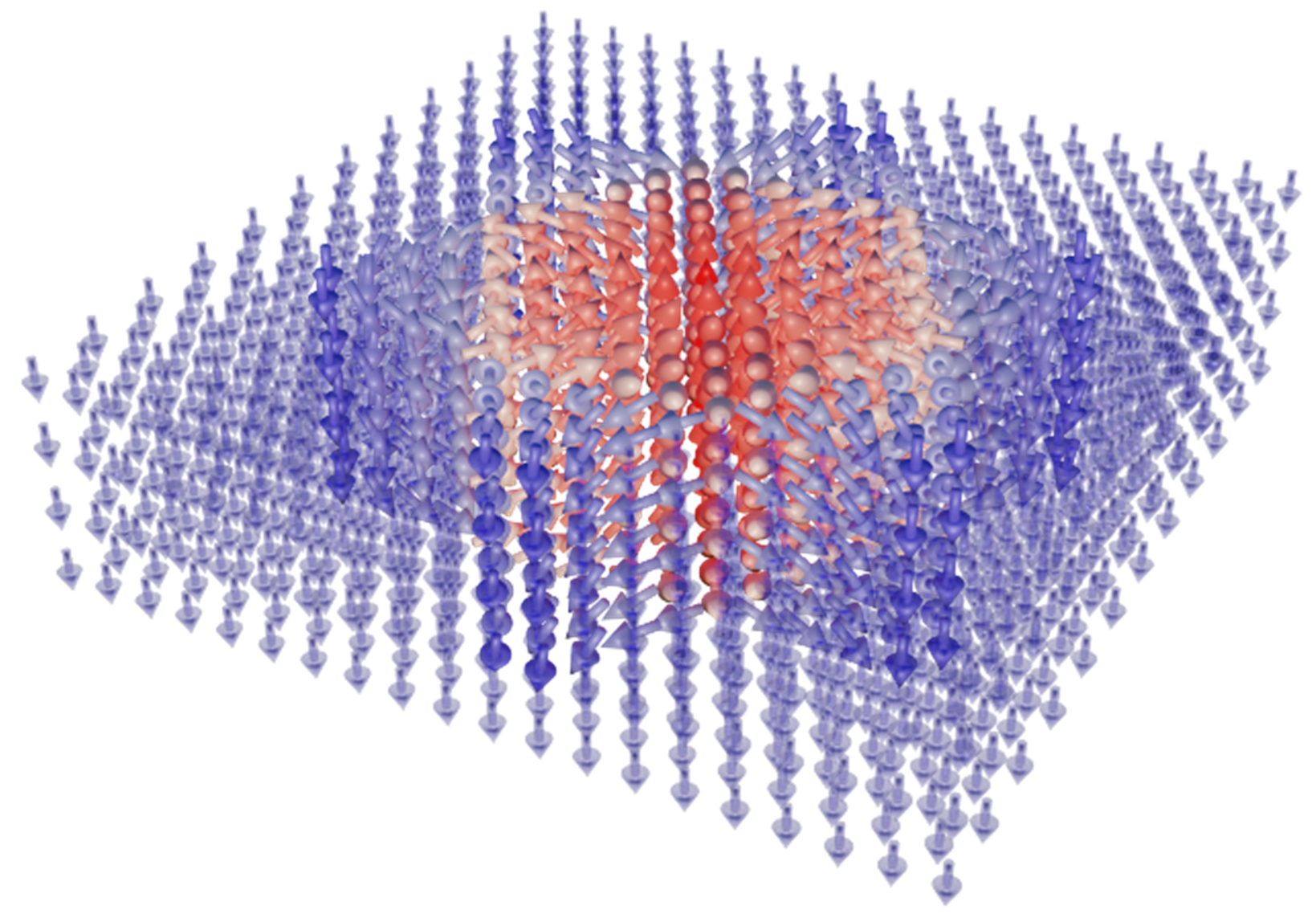
Figure: Polarization pattern of the ferroelectric antiskyrmion in rhombohedral BaTiO3 obtained from atomistic shell-model based computational experiment.
[1] S. Das, Y. L. Tang, Z. Hong, et al., Observation of room-temperature polar skyrmions, Nature 568, 368 (2019).
[2] M.A.P. Gonçalves, M. Paściak, and J. Hlinka, Antiskyrmions in ferroelectric barium titanate, Phys. Rev. Lett. 133, 066802 (2024).
(show less)
Discrepancy between microscopic quantum dynamics and macroscopic order in strongly correlated electron systems
We disclose a serious deficiency of the Baym-Kadanoff construction of thermodynamically consistent conserving approximations [Phys. Rev. B 109, 075171 (2024)].
We disclosed in this paper a long-neglected problem of matching microscopic quantum many-body dynamics with the macroscopic long-range order. The latter is presently derived from the former within the canonical Baym-Kadanoff construction of thermodynamically consistent conserving approximations. Two two-particle vertices, responsible for the system’s response to the external perturbations, must be introduced: microscopic dynamic and macroscopic conserving vertices. The former is determined from the diagrammatic perturbation theory, while the latter is obtained from the respective Ward identity, guaranteeing macroscopic conservation laws. The divergence of each vertex indicates an instability.
We revealed an ambiguity of the Baym-Kadanoff construction in determining the critical behavior with a transition to a thermodynamic long-range order. We demonstrated that each vertex leads to incomplete and distinct critical behavior with distinct instability points. The diagrammatically controlled dynamic vertex from the Schwinger-Dyson equation cannot directly be linked with a macroscopic long-range order, since it does not obey the Ward identity. Consequently, it cannot be continued beyond its instability. On the other hand, the divergence in the macroscopic vertex, obeying the conservation laws, has no direct microscopic consequences and does not invoke critical behavior of the spectral function and the specific heat as derived from the dynamic vertex. Consequently, the description of the critical behavior of correlated electrons becomes consistent and reliable only if the fluctuations of the order parameter in the conserving vertex lead to a divergence coinciding with that of the dynamical one. None of the existing approximate schemes fulfills this condition.
The ambiguity in the definition of phase instabilities of the Baym-Kadanoff scheme disclosed by us has a firm conclusion that an entirely consistent theory beyond the weak-coupling static Hartree-Fock approximation of the critical behavior of strongly correlated electrons is to be devised.
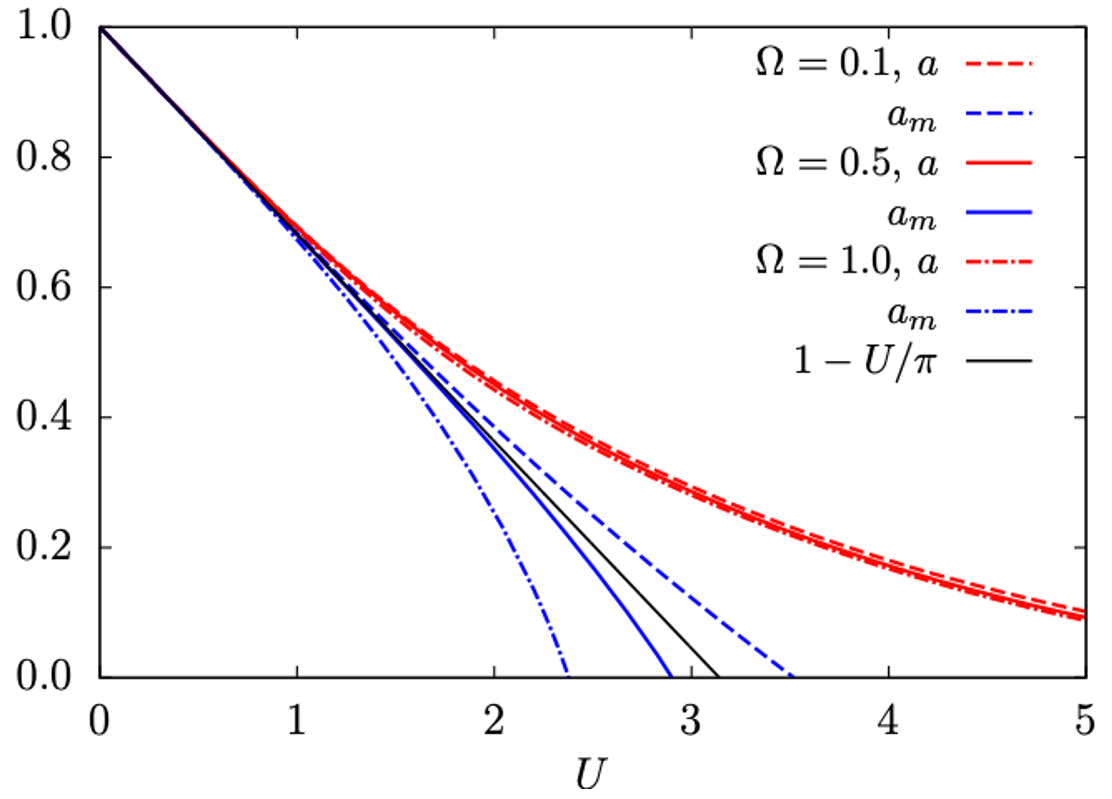
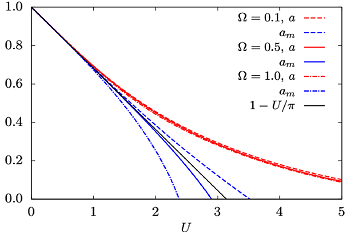
Demonstration of the ambiguity of the definition of phase instability. The dependence on the interaction strength U of the dimensionless Kondo scale a, measuring the distance to the magnetic instability from the dynamic vertex of the microscopic dynamic theory, red curves, and the Kondo scale from the macroscopic susceptibility am=χ0/χ, blue curves, plotted for different values of the ultraviolet cutoff in the polar approximation, accurate in determining the critical point, Ω; χ0,χ are zero-temperature bare and full susceptibilities. The black solid line is the Hartree static solution (1-U/π). Notice that the exact solution suppresses the magnetic instability, as obtained for the dynamic solution, red lines. The thermodynamic macroscopic criterion, blue lines, leads to a spurious instability, disqualifying the credibility of the dynamic approximations in determining consistently macroscopic instabilities of strongly correlated electrons.
[1] V. Janiš, V. Pokorný, and Š. Kos, Failure of the Baym-Kadanoff construction to consistently match quantum dynamics with thermodynamic critical behavior, Phys. Rev. B 109, 075171 (2024).
(show less)

Zigzag charged domain walls in ferroelectric PbTiO3
We report a theoretical investigation of a charged 180-degree domain wall in ferroelectric PbTiO3, compensated by randomly distributed immobile charge defects. We predict that domain walls form a zigzag pattern and we discuss their properties in a broad interval of compensation-region widths. The zigzag is accompanied by a local polarization rotation which we explain to provide an efficient mechanism for charge compensation [Phys. Rev. B 107, 094102 (2023)].
Our study delved into a theoretical exploration of charged domain walls in ferroelectric PbTiO3, which were compensated by randomly distributed immobile charge defects located within a relatively broad slab. To achieve this, we employed a combination of atomistic shell-model simulations and continuous phase-field simulations based on the Ginzburg-Landau-Devonshire model. Our findings showed that domain walls form a zigzag pattern, and we examined their properties across a broad range of compensation-region widths, ranging from a few nanometers to over 100 nm, focusing in particular on understanding the zigzag modulation lengths in terms of material properties of PbTiO3. The zigzag formation is accompanied by a local ferroelectric-polarization rotation, which we proposed as an efficient mechanism for local charge compensation. Our study provides a new understanding of the behavior of charged domain walls in ferroelectric materials and highlights the significance of the considered compensation charges in their formation. The insights gained from our study may contribute to the development of advanced ferroelectric materials with applications in the field of smart-materials for electronics.
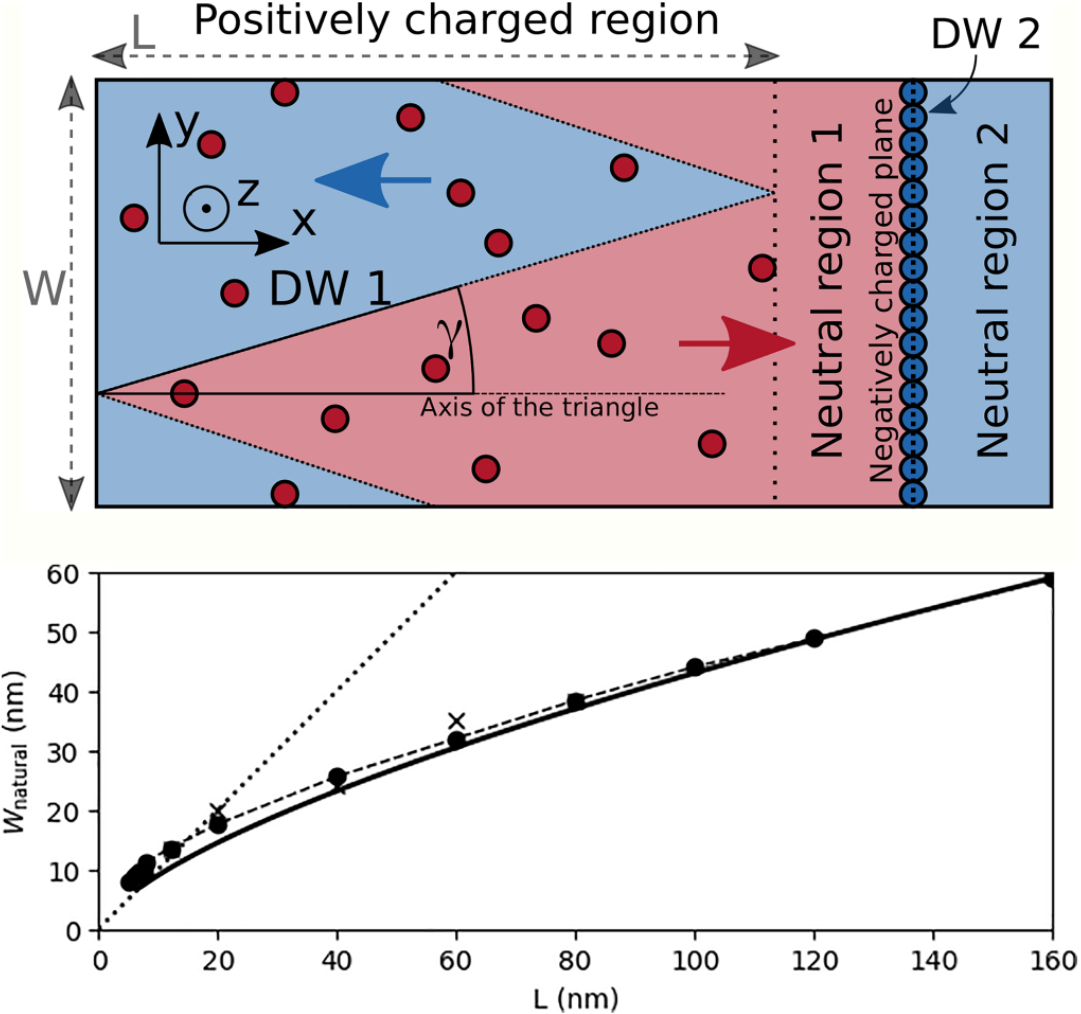
Figure:
Top panel: Schematic picture of the zigzag pattern, which is used in the derivation of natural width of triangles.
Red and blue colors and arrows correspond here to positively and negatively oriented ferroelectric domains
(with respect to the x axis). The color of the defects is red for positive and blue for negative point defects.
Bottom panel: Dependence of natural width of the zigzag triangles. Bullets: Phase-field simulations
with homogeneous compensation charge; the dashed line is just a connection of these.
Crosses: Phase-field simulations with randomly distributed defect charges.
Solid line: Simplified analytical model. Numerical and analytical approaches show
an excellent corespondence for large thicknesses of the compensation-region L.
[1] P. Marton, M. A. P. Gonçalves, M. Paściak, S. Körbel, V. Chumchal, M. Plešinger, A. Klíč, and J. Hlinka, Zigzag charged domain walls in ferroelectric PbTiO3, Phys. Rev. B 107, 094102 (2023).
(show less)
Out-of-equilibrium impurities with correlated electrons: Spectral and transport properties
We apply a two-particle semianalytic approach to a single Anderson impurity attached to two biased metallic leads. Furthermore, we qualitatively reproduce the three transport regimes with the increasing temperature: from the Kondo resonant tunneling through the Coulomb-blockade regime up to a sequential tunneling regime [Phys. Rev. B 105, 085122 (2022)].
Simple approximations to impurities with correlated electrons fail out of equilibrium, leading to an unphysical hysteresis loop in the current-voltage characteristics. Electron correlations are known to suppress this hysteresis. We applied a two-particle semianalytic approach to an out-of-equilibrium Anderson impurity attached to two biased metallic leads. The theory qualitatively correctly interpolates between weak and strong coupling. It is based on reduced parquet equations adapted to capture the critical regions of singularities in the Bethe-Salpeter equations. This advanced approach covers one-particle and two-particle thermodynamic and spectral quantities relatively well in both weak and strong coupling. Our approximation successfully suppressed the unphysical hysteresis loop. Furthermore, we qualitatively reproduced within the linear response the three transport regimes with the increasing temperature: from the Kondo resonant tunneling through the Coulomb-blockade regime up to a sequential tunneling regime. Far from equilibrium, we find that the bias plays a similar role as the temperature in destroying the Kondo resonant peak when the corresponding energy scale is comparable with the Kondo temperature. Aside from that, the applied voltage in low bias was shown to develop spectral peaks around the lead chemical potentials as observed in previous theoretical and experimental studies.
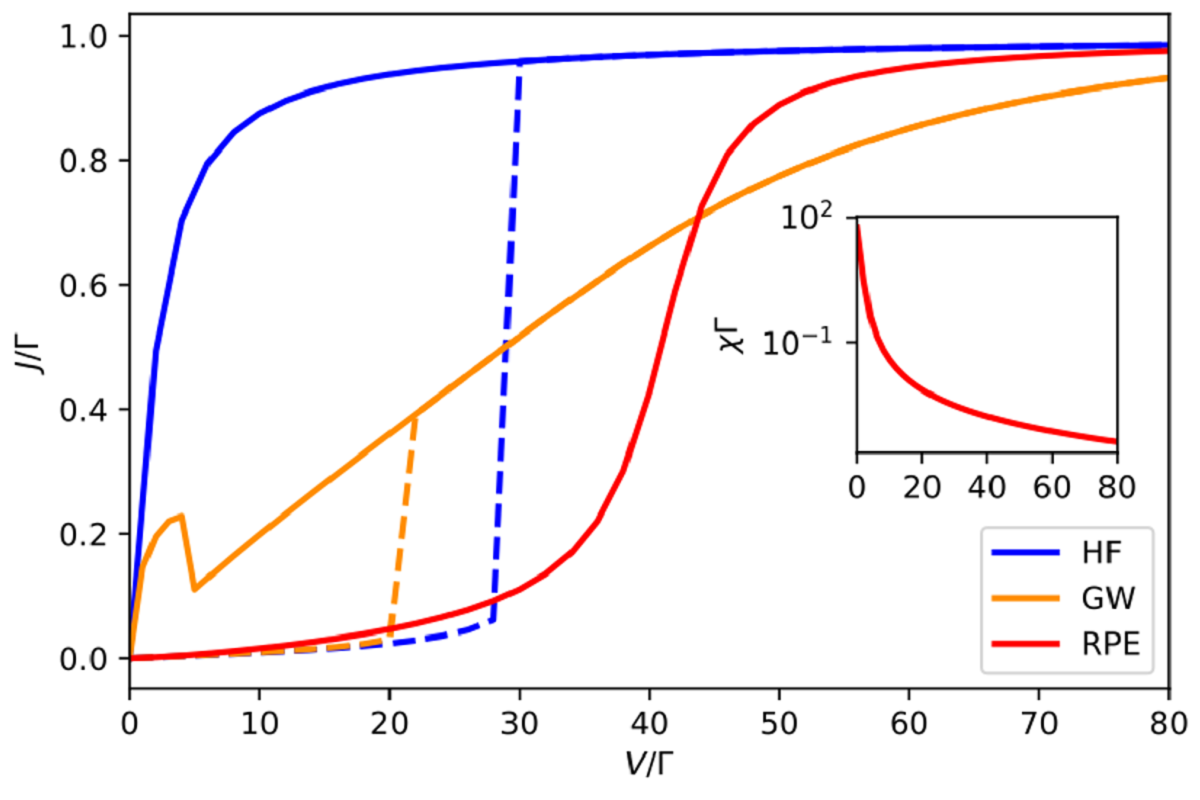
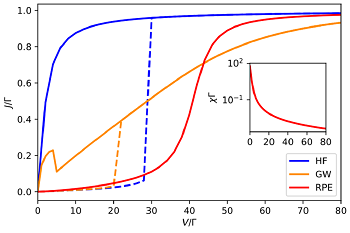
Figure: I-V characteristic curve of the Anderson impurity model at half-filling for interaction U = 40Γ and temperature T = 0.1Γ in the Coulomb-blockade regime calculated by the Hartree-Fock (HF) mean-field, GW approximation, and the reduced parquet equations (RPE). An unphysical hysteresis loop appears in the HF and GW approximations, with the solid line corresponding to the nonmagnetic solution and the dashed line to the magnetic one. The RPE suppresses the spurious magnetic order, hence it is free of hysteresis. Here, Γ is the energy unit, impurity bandwidth. The inset shows the magnetic susceptibility as a function of the bias voltage V.
[1] J. Yan and V. Janiš, Single-impurity Anderson model out of equilibrium: A two-particle semianalytic approach, Phys. Rev. B 105, 085122 (2022).
(show less)
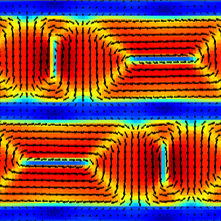
Multidomain ordered metal–ferroelectric superlattices
By combination of advanced experimental techniques and phase-field simulations, we found that electric dipoles in superlattices, composed of layers of a ferroelectric material separated by thin metallic spacers, form an unusual pattern of nanoscale domains that order in three dimensions. These ferroelectric multidomain ordered superlattices exhibit an outstanding dielectric response and their engineered modulated structural and electronic properties can be controlled using electric field [Nat. Mater. 20, 495 (2021)].
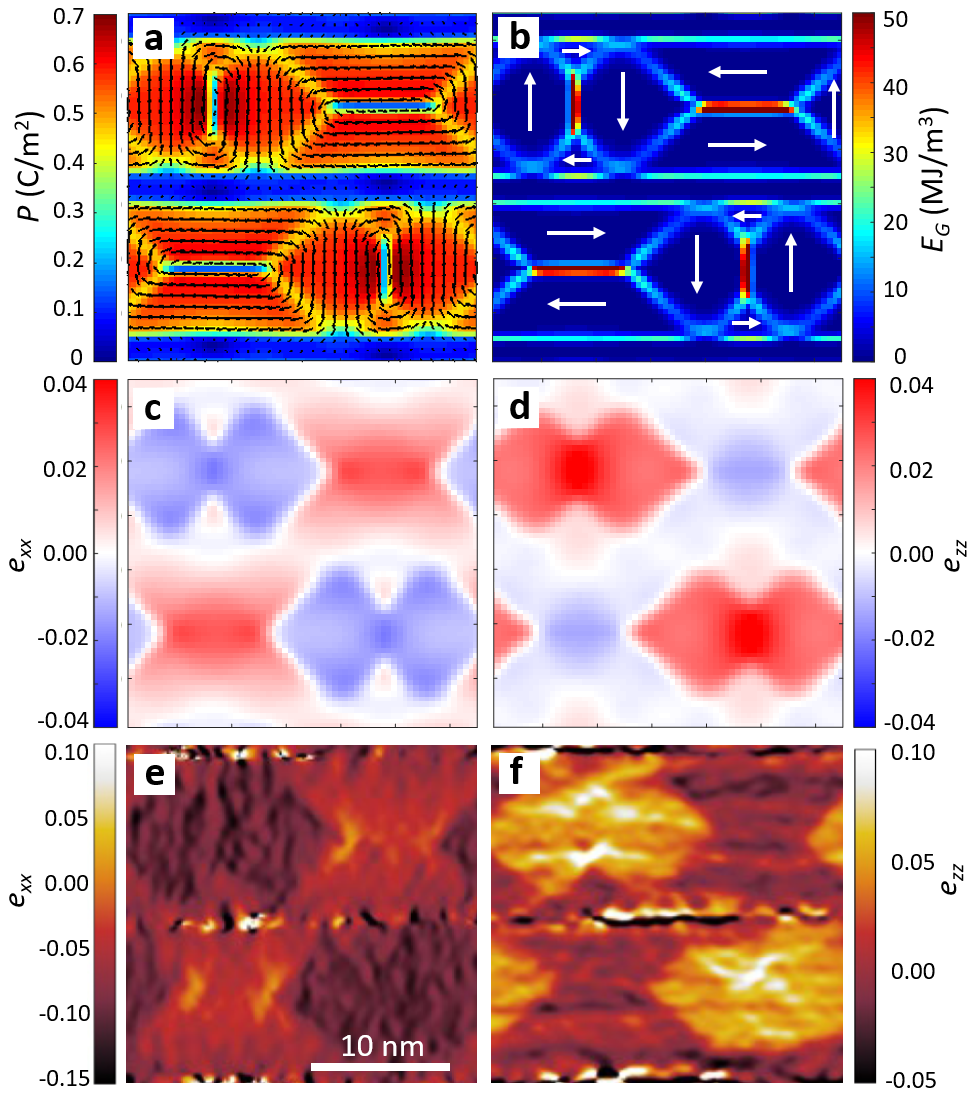
Figure:
Two-dimensional base motif of the ferroelectrically ordered PbTiO3–SrRuO3 superlattices as seen by
(a-d) phase-field simulations and (e,f) transmission electron microscopy:
(a) electric polarization showing ferroelectric domain structure in two PbTiO3 layers separated by SrRuO3 spacers
(b) gradient energy density coming from domain walls and boundaries between layers,
(c-f) in-plane (exx) and out-of-plane (ezz) strain components demonstrating correlations between ferroelectric PbTiO3 layers.
The arrows in (a,b) panels show direction of electric polarization forming characteristic flux-closure patterns.
[1] M. Hadjimichael, Y. Li, E. Zatterin, G. A. Chahine, M. Conroy, K. Moore, E. N. O’ Connell, P. Ondrejkovic, P. Marton, J. Hlinka, U. Bangert, S. Leake, and P. Zubko, Metal–ferroelectric supercrystals with periodically curved metallic layers, Nat. Mater. 20, 495 (2021).
(show less)
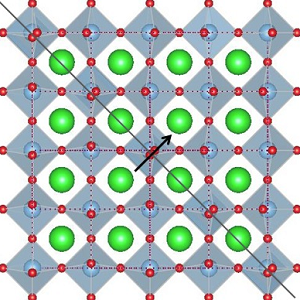
Polarization of domain boundaries in SrTiO3 studied by layer group and order-parameter symmetry
Based on a recently developed combination of layer group analysis with order-parameter symmetry, we study the polarity of antiphase domain boundaries (APBs) and ferroelastic twin boundaries (TBs) in SrTiO3 [Phys. Rev. B 102, 184101 (2020)].
In addition to the celebrated layer group analysis of domain twins, the present method allows us to investigate tensor properties of domain walls also for the case where order-parameter variables other than the spontaneous ones are active [1].
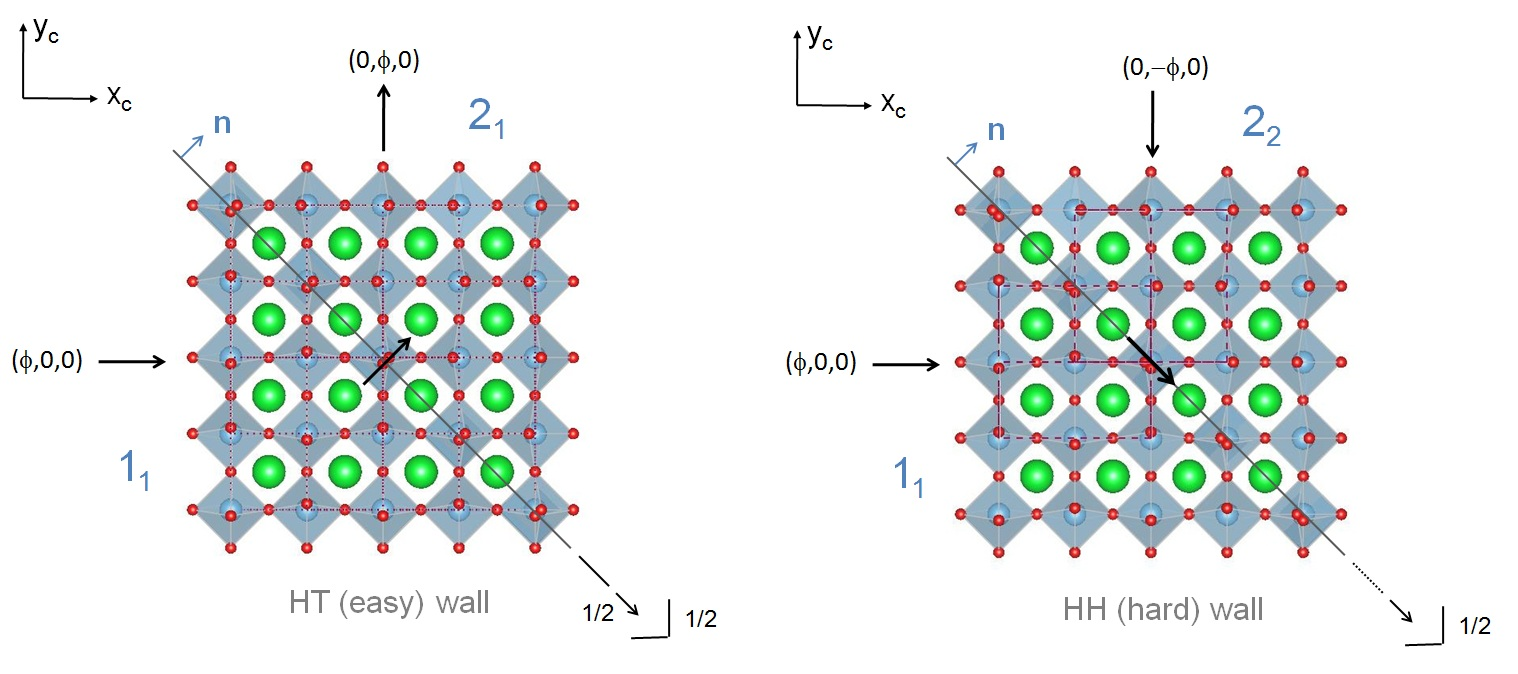
Figure: Representation of two different ferroelastic twins with normal n=[110] at position p=(0,0,0) in tetragonal SrTiO3, together with the symmetry elements of the corresponding layer groups. (a) Pure orientational twin (11|21). The corresponding twin wall is an easy (HT) wall. The twin in (b) is of mixed type, i.e., (11|22), where the corresponding twin wall is a hard (HH) one. The arrows at the centers show polarization predicted by the theory.
[1] W. Schranz, C. Schuster, A. Tröster, and I. Rychetský, Polarization of domain boundaries in SrTiO3 studied by layer group and order-parameter symmetry, Phys. Rev. B 102, 184101 (2020). (show less)
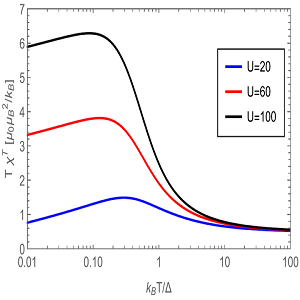
Curie-Weiss susceptibility in strongly correlated electron systems
We succeeded in identifying a microscopic mechanism combining adequately quantum and thermal fluctuations in metals with strong electron correlations that lead to the genesis of local magnetic moments and the Curie-Weiss susceptibility [Phys. Rev. B 102, 205120 (2020)].
The magnetism of solids is macroscopic evidence of microscopic quantum dynamics of spins of valence electrons. Magnetic susceptibility of metals with delocalized conduction electrons should theoretically be of Pauli character. However, the transition metals react on the magnetic field via the Curie-Weiss law due to local magnetic moments. We identified the microscopic mechanism combining adequately quantum and thermal fluctuations in metals with strong electron correlations that lead to the genesis of local magnetic moments and the Curie-Weiss susceptibility [1].
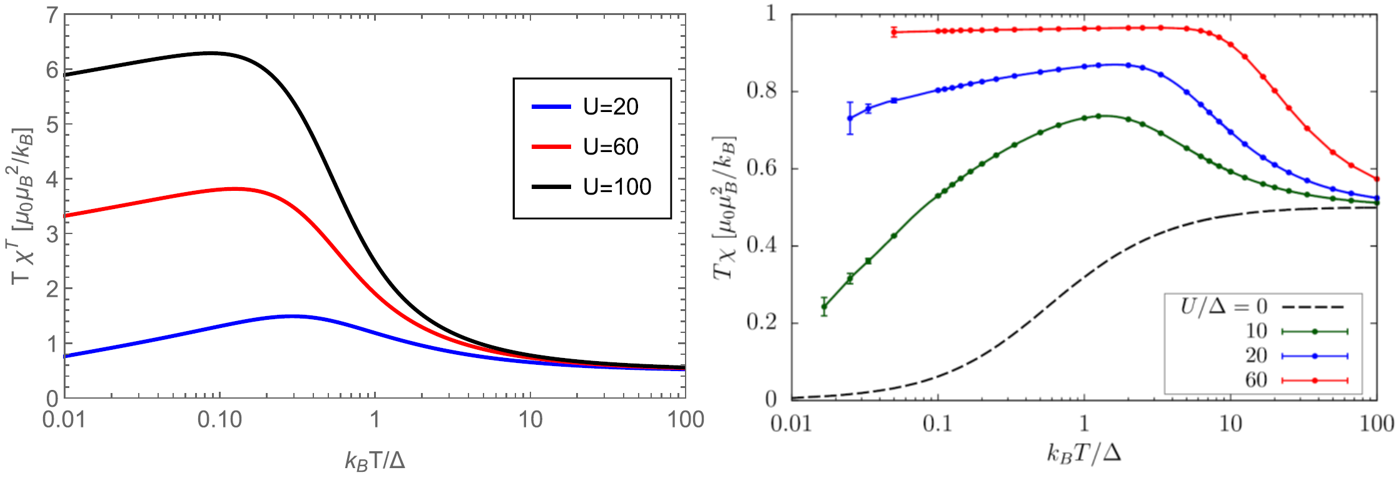
Figure: Temperature dependence of the product of temperature T and magnetic susceptibility χ, the constant value of which reflects the Curie-Weiss law, determined from our analytic theory, left panel, and from Monte-Carlo simulations, right panel, for the single-impurity Anderson model. Here Δ is the width of the band of the conduction electrons, and U is the strength of electron correlations. Both results prove the existence of the Curie-Weiss susceptibility for sufficiently strong electron correlations in a temperature interval above the Kondo temperature below which the susceptibility goes over to the Pauli one, and the plotted curves must fall to zero. The analytic theory predicts qualitatively correctly the universal character of the Curie-Weiss susceptibility but misses the nonuniversal numerical value of the Curie constant.
[1] V. Janiš, A. Klíč, J. Yan, and V. Pokorný, Curie-Weiss susceptibility in strongly correlated electron systems, Phys. Rev. B 102, 205120 (2020). (show less)

Local properties and phase transitions in Sn doped antiferroelectric PbHfO3 single crystal
Pb(Hf0.77Sn0.23)03 crystals were characterized using x-ray diffraction and 119Sn Mossbauer spectroscopy in a wide temperature range. The nature of two intermediate phases, situated between antiferroelectric ground-state and high temperature paraelectric phase, has been unveiled [J. Phys.: Condens. Matter 32, 435402 (2020)].
The lower-temperature one is characterized by incommensurate modulations while the higher-T intermediate phase is defined by anti-phase rotations of oxygen octahedra. Two kinds of quadrupole splitting indicate that the environment of Sn is locally non-centrosymmetric even in the cubic phase [1].
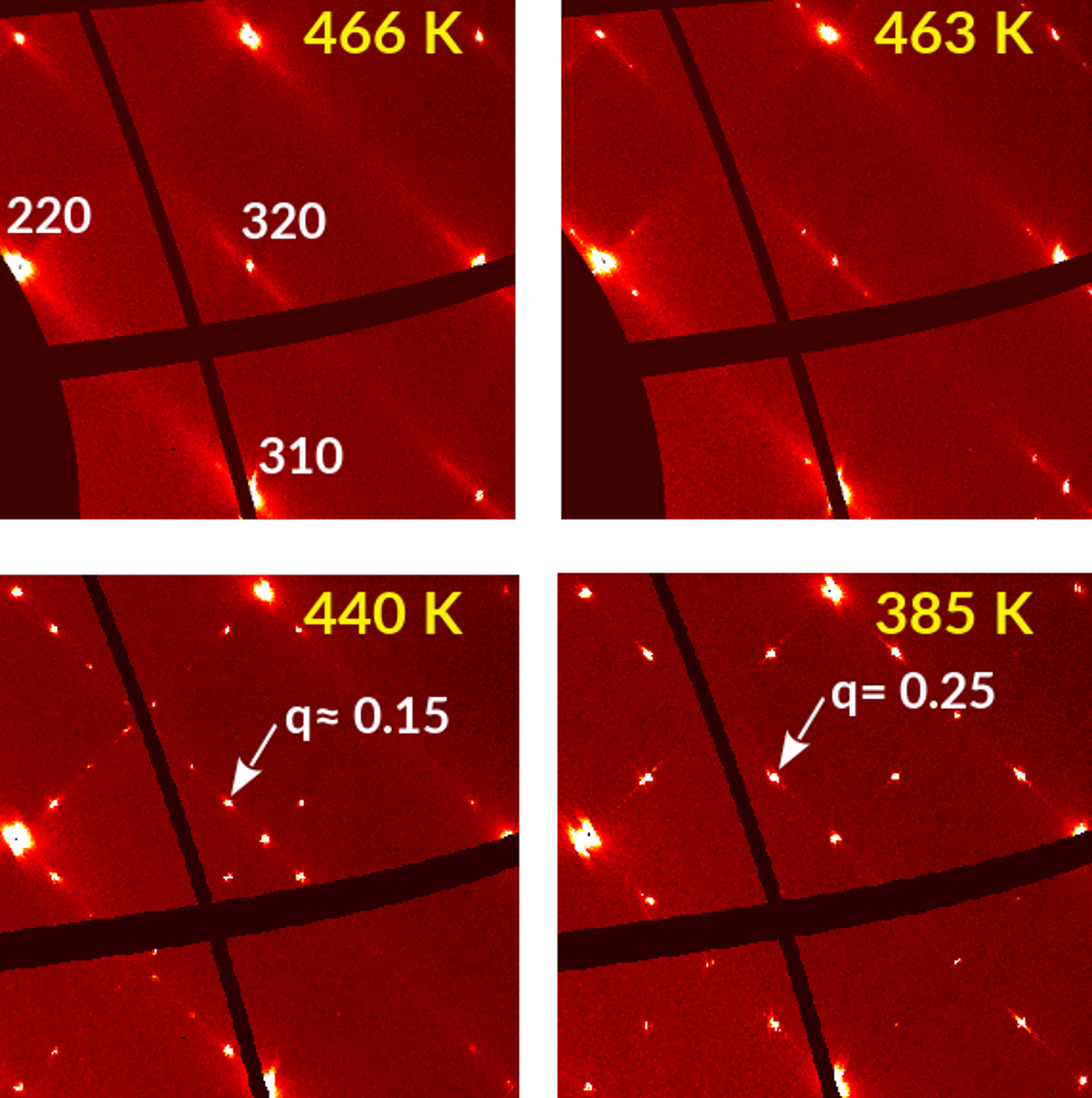
Figure: Diffraction signatures of four phases observed for Pb(Hf0.77Sn0.23)03. Diffuse streaks emerging from Bragg reflections at high temperatures are a signature of disorder (locally correlated displacements of Pb ions). They transform into broad maxima at 463 K, incommensurate peaks at 440 K and finally commensurate Bragg reflections at 385 K in the ground-state phase of this material.
[1] I. Jankowska-Sumara, M. Paściak, M. Kądziołka-Gaweł, M. Podgórna, A. Majchrowski, and K. Roleder, Local properties and phase transitions in Sn doped antiferroelectric PbHfO3 single crystal, J. Phys.: Condens. Matter 32, 435402 (2020). (show less)
Spatio-temporal distribution of relative Ti-O6 displacements in cubic BaTiO3
BaTiO3 is often considered a model ferroelectric material in which the dielectric properties are defined by the displacements of Ti ions with respect to surrounding oxygen atoms. However, despite the decades of a dedicated research, certain controversies have remained as to the description of collective movements of the Ti ions. We approached this problem using nonoscale-oriented X-ray scattering methods and large-scale atomistic simulations [1]. Together these allowed us to show that the Ti dynamics can be exhaustively explained by phonons excited on a timescale of picoseconds.
The three-dimensional distribution of the x-ray diffuse scattering intensity of BaTiO3 has been recorded in a synchrotron experiment and simultaneously computed using molecular dynamics simulations of a shell model. Together, these have allowed the details of the disorder in paraelectric BaTiO3 to be clarified. The narrow sheets of diffuse scattering, related to the famous anisotropic longitudinal correlations of Ti ions, are shown to be caused by the overdamped anharmonic soft phonon branch. This finding demonstrates that the occurrence of narrow sheets of diffuse scattering agrees with a displacive picture of the cubic phase of this textbook ferroelectric material. The presented methodology allows one to go beyond the harmonic approximation in the analysis of phonons and phonon-related scattering.
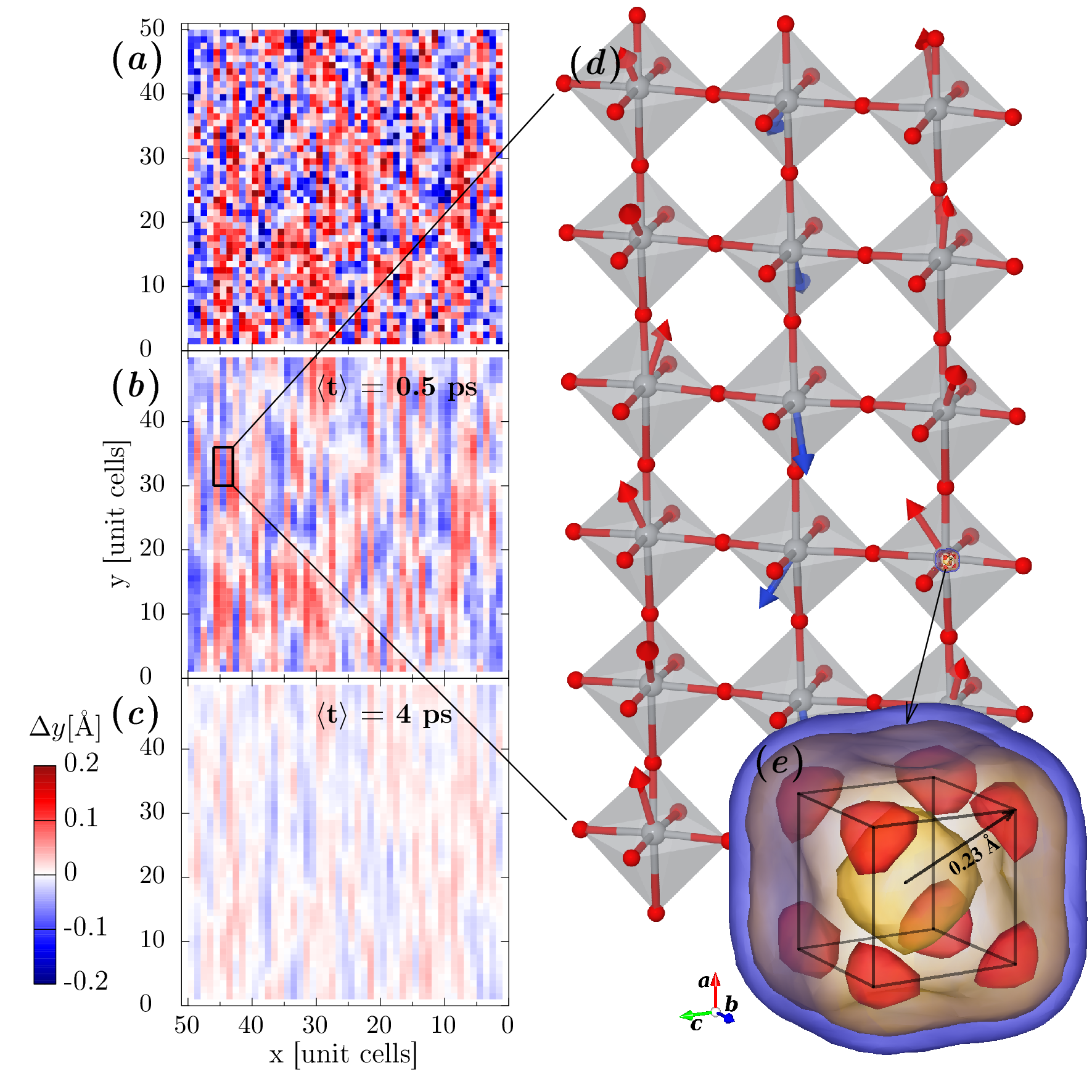
Fig. 1: One component of the relative Ti-O6 displacement is mapped within one layer of the material using different time averages (a-c) which clearly shows that chain correlations exist on a timescale of picoseconds. The displacements averaged over the simulation time and all unit cells of the crystal have a cuboidal distribution with shallow minima along diagonal directions.
[1] M. Paściak, T. R. Welberry, J. Kulda, S. Leoni, and J. Hlinka, Dynamic Displacement Disorder of Cubic BaTiO3, Phys. Rev. Lett. 120, 167601 (2018).
(show less)
Domain wall contribution to lattice dynamics and permittivity of BiFeO3
Ferroelectric materials are known for their exceptionally high dielectric permittivity. It turns out, that important part of it originates from a material's complicated microstructure and in particular from interfaces between ferroelectric domains.
In this study we investigate different types of interfaces in a multiferroic BiFeO3. By means of atomistic modelling we show that some configurations of interfaces can greatly enhance the permittivity by hosting terahertz-range collective polar fluctuations. The key result is that the permittivity is modified in the THz range. This fundamental finding and its understanding can be used in a design of new materials [ J. Hlinka, M. Pasciak, S. Körbel, and P. Márton, Phys. Rev. Lett. 119, 057604 (2017) ].
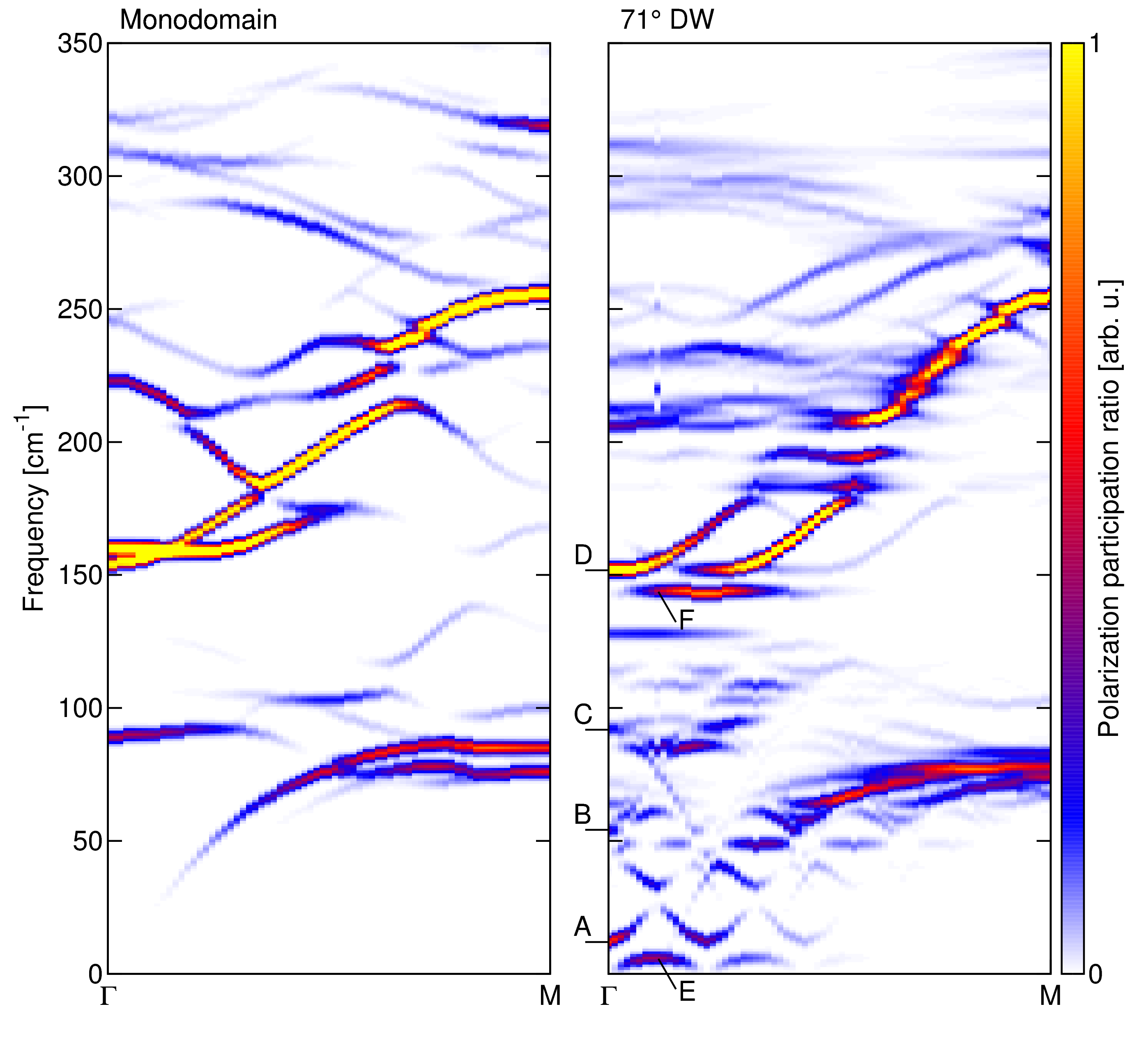
Figure: Change of the phonon spectrum due to presence of dense domain-interface structure (right panel) in comparison with the single-domain case (left panel). Change of the (polar-active) phonon spectrum due to presence of dense domain-interface structure of BiFeO3 (right panel) in comparison with the single-domain case (left panel). Additional low-frequency Γ-point mode (labelled A) is responsible for 25x enhancement of permittivity in the domain engineered material.
First-principles-based Landau-Devonshire potential for BiFeO3
We describe a first-principles-based computational strategy for determination of the Landau-Devonshire potential.
It exploits the configuration space attached to the eigenvectors of the modes frozen in the ground state. This allows to probe the energy surface in the vicinity of the ground state, which is most relevant for the properties of the ordered phase. We apply this procedure to BiFeO3 in order to determine potential energy associated with strain, polarization, and oxygen octahedra tilt. [ P. Marton, A. Klíč, M. Paściak, and J. Hlinka, Phys. Rev. B 96, 174110 (2017) ].
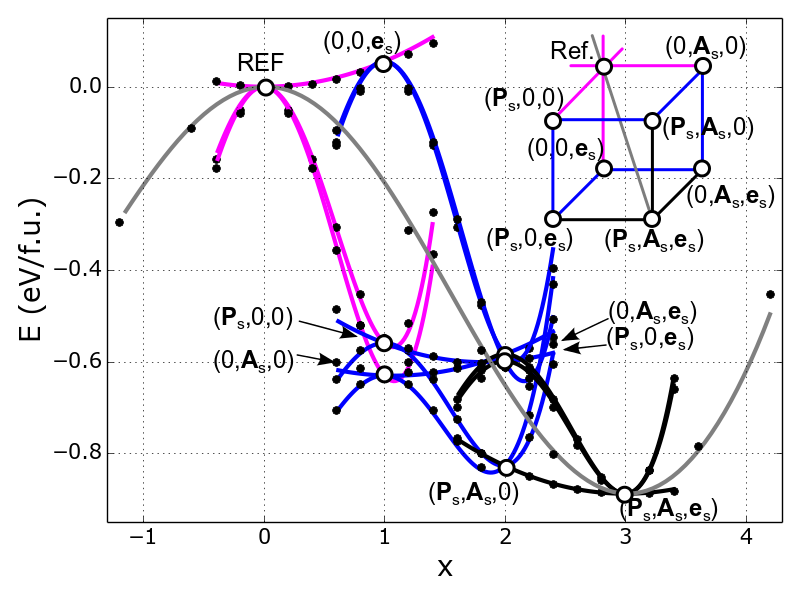
Figure: Energy profiles along selected paths in order parameter space of BiFeO3, connecting the cubic reference state (REF) and the ground state (Ps , As , es). Point symbols are outcomes of the first-principles calculations, lines are evaluated from the present Landau-Devonshire potential.
Existence conditions for ferroaxial materials
All 212 species of structural phase transitions with a macroscopic symmetry breaking were inspected with respect to the simultaneous occurrence of the ferroelastic, ferroelectric, and ferroaxial properties.
For each species, a matrix of representative equilibrium property tensors in both high-symmetry and low-symmetry phases, showing emergence of spontaneous components, were explicitly worked out [http://palata.fzu.cz/species/13x13axial]. Results can serve as a useful tool in search of fundamentally new material properties [J. Hlinka et al., Phys. Rev. Lett. 116, 177602 (2016)].
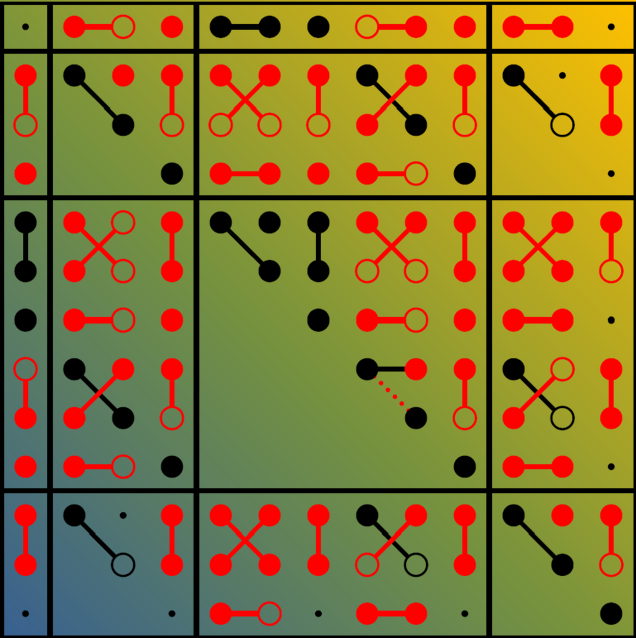
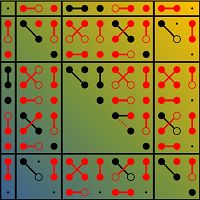
Figure: Dichromatic matrix of material property tensors for a symmetry-breaking structural phase transition from tetragonal to monoclinic phases, showing relations between tensor components of both phases and emergence of spontaneous components (red points).
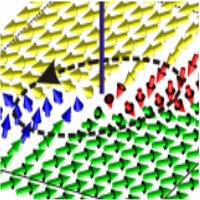
Ising lines: Natural topological defects within ferroelectric Bloch walls
Phase-field simulations demonstrate that the polarization order-parameter field in the Ginzburg-Landau-Devonshire model of rhombohedral ferroelectric BaTiO3 allows for an interesting linear defect, stable under simple periodic boundary conditions. This linear defect, here called the Ising line, can be described as an about 2-nm-thick intrinsic paraelectric nanorod acting as a highly mobile borderline between finite portions of Bloch-like domain walls of opposite helicity.
These Ising lines play the role of domain boundaries associated with the Ising-to-Bloch domain-wall phase transition. Therefore, the electric field parallel to the Ising line can be used to induce the Ising line motion, which mediates the switching of both polarization and chirality of the Bloch wall without changing the bulk domain polarization. Detailed description of this study can be found in the paper [ V. Stepkova, P. Marton, and J. Hlinka, Phys. Rev. B 92, 094106 (2015)]
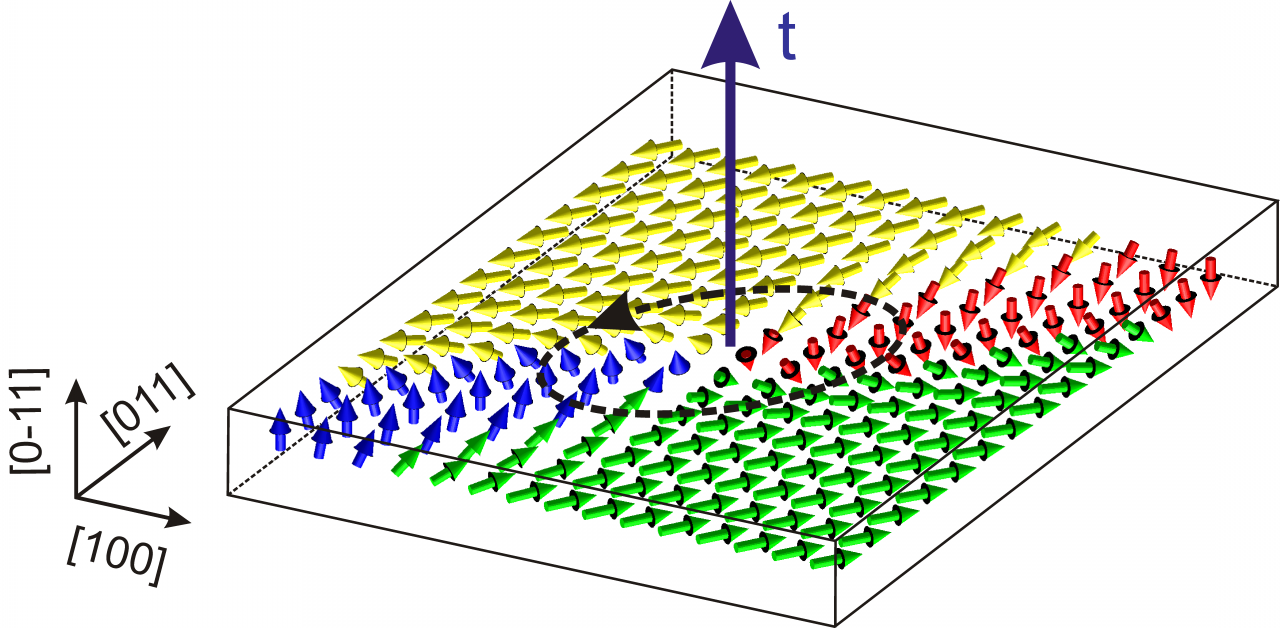
Figure: Ising line defect in rhombohedral BaTiO3. When circumventing the core of this defect following a closed path (dashed line) around its axis t, the polarization on this path rotates around the [-211] axis, which is perpendicular to t.
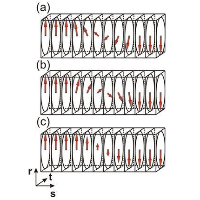
Phase transition in ferroelectric domain walls of BaTiO3
The seminal paper by Zhirnov (1958 Zh. Eksp. Teor. Fiz. 35 1175–80) explained why the structure of domain walls in ferroelectrics and ferromagnets is so different. We have recently realized that the antiparallel ferroelectric walls in rhombohedral ferroelectric BaTiO3 can be switched between the Ising-like state (typical for ferroelectrics) and a Bloch-like state (unusual for ferroelectric walls but typical for magnetic ones) [see Figure 1] by a compressive epitaxial stress.
Phase-field simulations using a Ginzburg–Landau–Devonshire model allows to explore this strain-induced phase transition within the domain wall in detail [Figure 2]. Strain-tunable chiral properties of ferroelectric Bloch walls promise a range of novel phenomena in epitaxial ferroelectric thin films. Results are published in JPCM [ V. Stepkova et al., J. Phys.: Condens. Matter 24, 212201 (2012)].
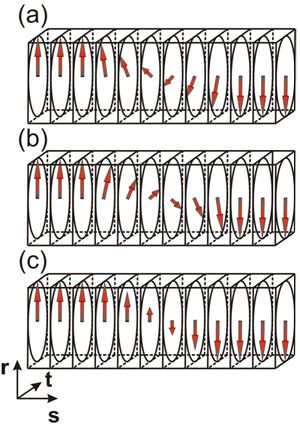
Figure 1: Variation of polarization P within Bloch- and Ising-type domain walls. The Bloch-type structure (a,b) conserves the magnitude of the local vectorial order parameter. This is typically encountered in ferromagnetism. In contrast, ferroelectric materials usually have large anisotropy and the magnitude of the polarization can be more easily adjusted. Therefore, antiparallel walls in ferroelectrics are known to correspond to the achiral Ising solution (c). We show here that in rhombohedral BaTiO3, both types of 180° domain walls can be stabilized.
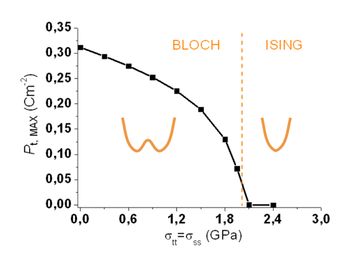
Figure 2: Chiral order parameter. The extremal value of the Pt polarization component in the core of the domain wall is plotted as a function of the epitaxial stress. This quantity can be taken as an order parameter of this chiral phase transition within the domain wall. For the wall under study, the phase transition is continuous and it can be associated with the Landau free-energy sketched in the figure.
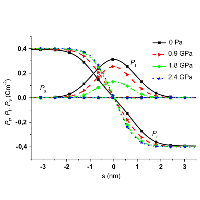
Dielectric response of a phase transition in domain wall
Computer simulations based on Ginzburg-Landau-Devonshire theory was used to study details of a phase-transition between Ising and Bloch type of a domain wall.
Such transition was predicted to appear for 180 degree domain wall in the rhombohedral ferroelectric phase of BaTiO3 close to 2GPa compressive stress [ V. Stepkova et al., J. Phys.: Condens. Matter 24, 212201 (2012)]. We confirm the hypothesis that the phase transition is of the first-order and predict corresponding divergent increase of the dielectric permittivity in the vicinity of the transition. In case of dense domain-wall pattern it can represent a substantial part of the dielectric response of the material [ P. Marton et al., Phase Transitions 86, 103 (2012)].
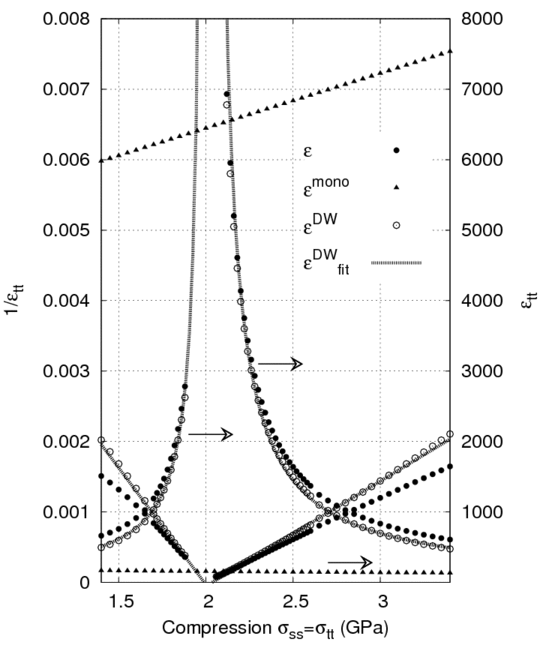
Figure 1: Dielectric permittivity in dependence on mechanical pressure in the vicinity of the transition from Ising (larger pressure) to Bloch-type of the domain wall.
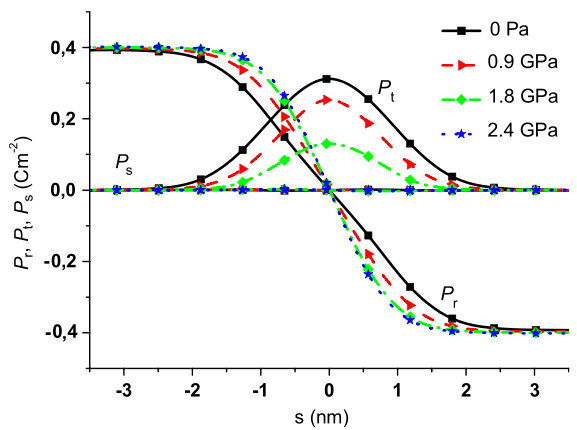
Figure 2: Bloch-to-Ising phase transition within a rhombohedral 180° domain wall.
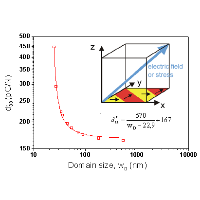
Piezoelectric response of nanotwinned ferroelectric perovskites
Computer simulations based on Ginzburg-Landau-Devonshire theory has benn used to investigate piezoelectric properties of tetragonal BaTiO3 crystals. We have shown that piezoelectric response of twinned BaTiO3 increases with increasing density of 90-degree domain walls.
A considerable enhancement of piezoelectric coefficients is predicted below 50 nm. We have also shown that main contribution to the longitudinal piezoelectric coefficient comes from volume of domain, rather than from the domain wall region. Nevertheless, the experimentally reported impact of domain wall density is even stronger than in our simulations. Our most recent theoretical investigations [P. Marton et al, Physical Review B 81, 144125 (2010)] suggest that ferroelectric perovskites such as BaTiO3 most likely support also more exotic domain walls, resembling Bloch walls known from ferromagnetism. This kind of domain walls might account for additional enhancement of the electromechanical material response.
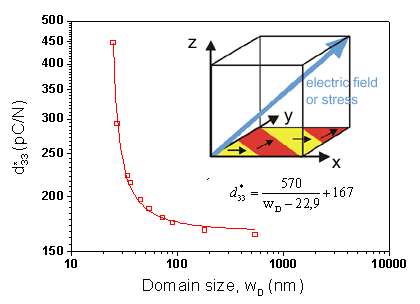
Figure 1: Dependence of the effective longitudinal piezoelectric coefficient on domain size calculated from the response of the ideal 2D laminar domain structure to weak uniaxial stresses applied along the [111] crystallographic direction. The inset shows the geometry of the initial 2D laminate domain structure assumed in the simulations.
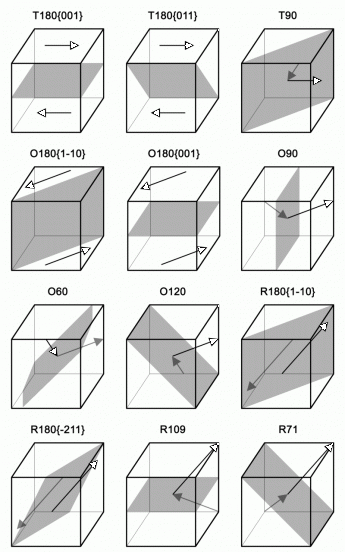
Figure 2: Set of mechanically compatible and electrically neutral domain walls in the three ferroelectric phases o f BaTiO3. Letter denominating the phase (T, O and R stay for tetragonal, orthorhombic and rhombohedral phase, resp.) is followed by an angle between the polarization in adjacent domains and in some cases also by the domain-wall normal.