Topological structures
Pyramidal charged domain walls in ferroelectric BiFeO3
We uncover the physical origins of the enigmatic zigzag domain structure in the prototypical multiferroic material BiFeO3. Using phase-field simulations, we demonstrate that spatially-homogeneous defect charges result in domain structures that closely resemble those observed experimentally. The acquired understanding of the underlying physics of pyramidal-domain formation may enable the engineering of new materials with self-assembled domain structures. [Commun. Mater. 6, 161 (2025)].
We addressed a long-standing puzzle in ferroelectric research: the origin of unusual zigzag and pyramidal domain structures in the multiferroic material BiFeO3. These complex patterns had been observed experimentally for years, but their physical cause remained unclear. Using phase-field simulations within the Landau–Ginzburg–Devonshire framework, we demonstrated that they can naturally form when defect charges are distributed homogeneously in the crystal. The system compensates these charges by creating pyramid-like domains in which the polarization rotates to lower the overall energy. Our simulated patterns agree closely with transmission electron microscopy observations of BiFeO3 crystals from our colleagues at the University of Warwick, giving strong support to our model. Beyond solving a fundamental question, this insight has practical value. The pyramidal domains are highly regular and self-assembled with nanometer-scale periodicity, making them attractive for applications requiring precise ordering, such as optics or topological defect-based devices.
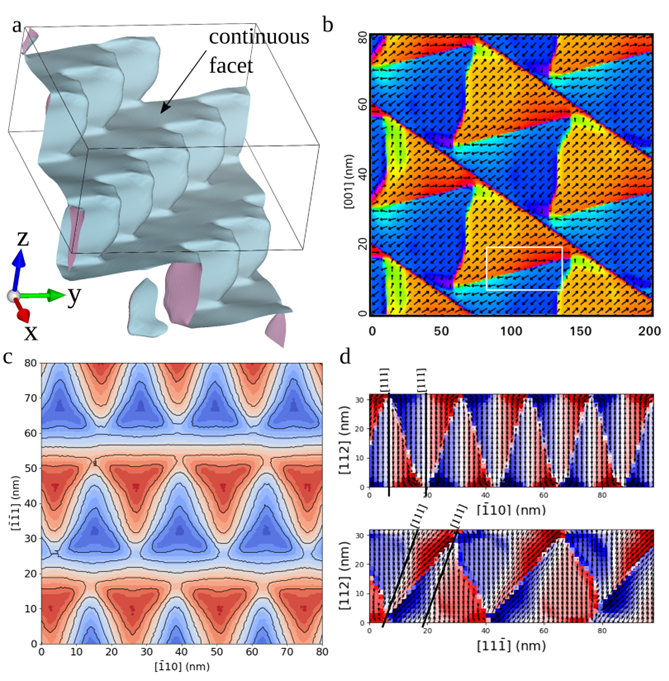
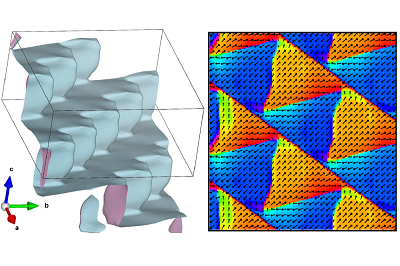
Phase-field simulations for a rhombohedral ferroelectric material:
a) 3D visualization of the wall surface.
b) Ferroelectric polarization visualized in the plane (-110).
c) Distance of the domain wall from the center of the charged layer measured along [111].
d) Deviation of the polarization from the pyramid’s axis.
Polarization is projected to two selected planes, color indicates polarization component perpendicular to [111] direction.
Red: positive, blue: negative, white: no deviation.
[1] P. Marton, M. Paściak, M. A. P. Gonçalves, O. Novák, J. Hlinka, R. Beanland, and M. Alexe, Pyramidal charged domain walls in ferroelectric BiFeO3, Commun. Mater. 6, 161 (2025).
(show less)
Antiskyrmions in ferroelectric barium titanate
Our recent molecular dynamics computational study reveals that the bulk crystal of the archetypal ferroelectric perovskite BaTiO3 can host ferroelectric antiskyrmions at zero field. We show that the antiskyrmion has just 2-3 nm in diameter and that it carries a very exotic topological charge of minus two [Phys. Rev. Lett. 133, 066802 (2024)].
The prediction and experimental confirmation of magnetic skyrmions revolutionized the physics of nanoscale magnetism and opened new horizons for spintronics. In spite the inherently shorter and faster correlations of the electric polarization and challengingly smaller correlation lengths, the recent developments in electric skyrmionics follow these innovations. It is only 5 years since the first observation of a ferroelectric skyrmion in thin lead-strontium titanate superlattices [1].
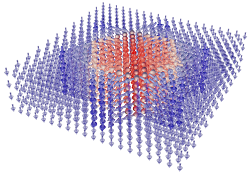
The present molecular dynamics computational study [2)] reveals that the bulk crystal of the archetypal ferroelectric perovskite (barium titanate) can host peculiar 2-3 nm wide standalone polar columns stable till temperatures of several tens of Kelvins. They are spontaneously surrounded by a unique noncollinear polarization pattern (see figure) that has never been described before. We explained how and why this pattern is formed and stabilized. Since its invariant skyrmion topological charge is an integer with a sign opposite to that of the usual skyrmions, they named this soliton as ferroelectric antiskyrmion. They clarify that formation of antiskyrmions consists in breakdown of high-curvature 180-degree ferroelectric walls into triplets of lower-energy 71-degree walls. It is explained that this process is favored by a fortunate combination of the moderate anisotropy of the anharmonic electric susceptibility and the pronounced anisotropy of the polarization correlations in barium titanate crystals. These findings represent a clear milestone in the studies of topological defects in ferroelectrics.
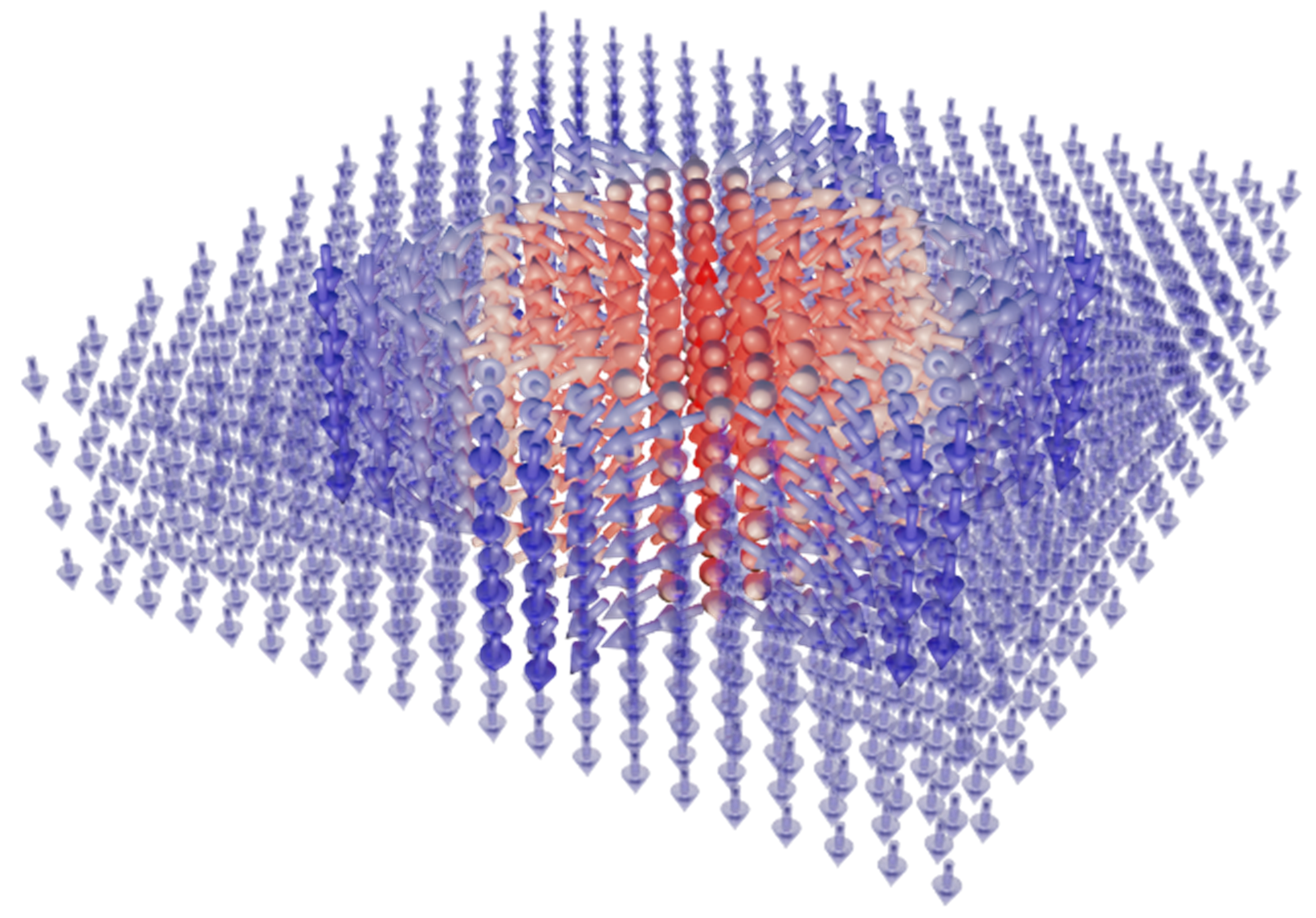
Figure: Polarization pattern of the ferroelectric antiskyrmion in rhombohedral BaTiO3 obtained from atomistic shell-model based computational experiment.
[1] S. Das, Y. L. Tang, Z. Hong, et al., Observation of room-temperature polar skyrmions, Nature 568, 368 (2019).
[2] M.A.P. Gonçalves, M. Paściak, and J. Hlinka, Antiskyrmions in ferroelectric barium titanate, Phys. Rev. Lett. 133, 066802 (2024).
(show less)

Zigzag charged domain walls in ferroelectric PbTiO3
We report a theoretical investigation of a charged 180-degree domain wall in ferroelectric PbTiO3, compensated by randomly distributed immobile charge defects. We predict that domain walls form a zigzag pattern and we discuss their properties in a broad interval of compensation-region widths. The zigzag is accompanied by a local polarization rotation which we explain to provide an efficient mechanism for charge compensation [Phys. Rev. B 107, 094102 (2023)].
Our study delved into a theoretical exploration of charged domain walls in ferroelectric PbTiO3, which were compensated by randomly distributed immobile charge defects located within a relatively broad slab. To achieve this, we employed a combination of atomistic shell-model simulations and continuous phase-field simulations based on the Ginzburg-Landau-Devonshire model. Our findings showed that domain walls form a zigzag pattern, and we examined their properties across a broad range of compensation-region widths, ranging from a few nanometers to over 100 nm, focusing in particular on understanding the zigzag modulation lengths in terms of material properties of PbTiO3. The zigzag formation is accompanied by a local ferroelectric-polarization rotation, which we proposed as an efficient mechanism for local charge compensation. Our study provides a new understanding of the behavior of charged domain walls in ferroelectric materials and highlights the significance of the considered compensation charges in their formation. The insights gained from our study may contribute to the development of advanced ferroelectric materials with applications in the field of smart-materials for electronics.
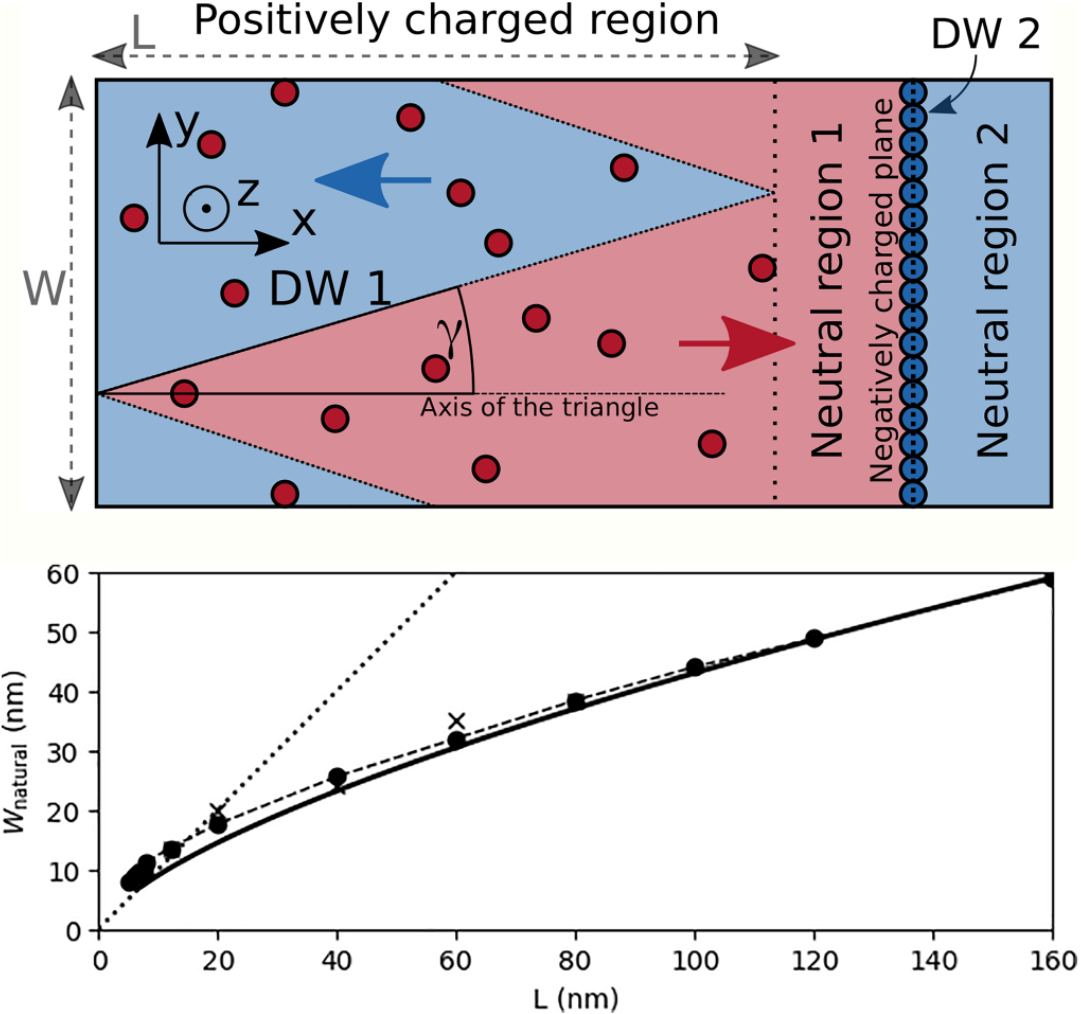
Figure:
Top panel: Schematic picture of the zigzag pattern, which is used in the derivation of natural width of triangles.
Red and blue colors and arrows correspond here to positively and negatively oriented ferroelectric domains
(with respect to the x axis). The color of the defects is red for positive and blue for negative point defects.
Bottom panel: Dependence of natural width of the zigzag triangles. Bullets: Phase-field simulations
with homogeneous compensation charge; the dashed line is just a connection of these.
Crosses: Phase-field simulations with randomly distributed defect charges.
Solid line: Simplified analytical model. Numerical and analytical approaches show
an excellent corespondence for large thicknesses of the compensation-region L.
[1] P. Marton, M. A. P. Gonçalves, M. Paściak, S. Körbel, V. Chumchal, M. Plešinger, A. Klíč, and J. Hlinka, Zigzag charged domain walls in ferroelectric PbTiO3, Phys. Rev. B 107, 094102 (2023).
(show less)
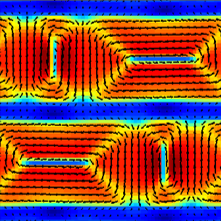
Multidomain ordered metal–ferroelectric superlattices
By combination of advanced experimental techniques and phase-field simulations, we found that electric dipoles in superlattices, composed of layers of a ferroelectric material separated by thin metallic spacers, form an unusual pattern of nanoscale domains that order in three dimensions. These ferroelectric multidomain ordered superlattices exhibit an outstanding dielectric response and their engineered modulated structural and electronic properties can be controlled using electric field [Nat. Mater. 20, 495 (2021)].
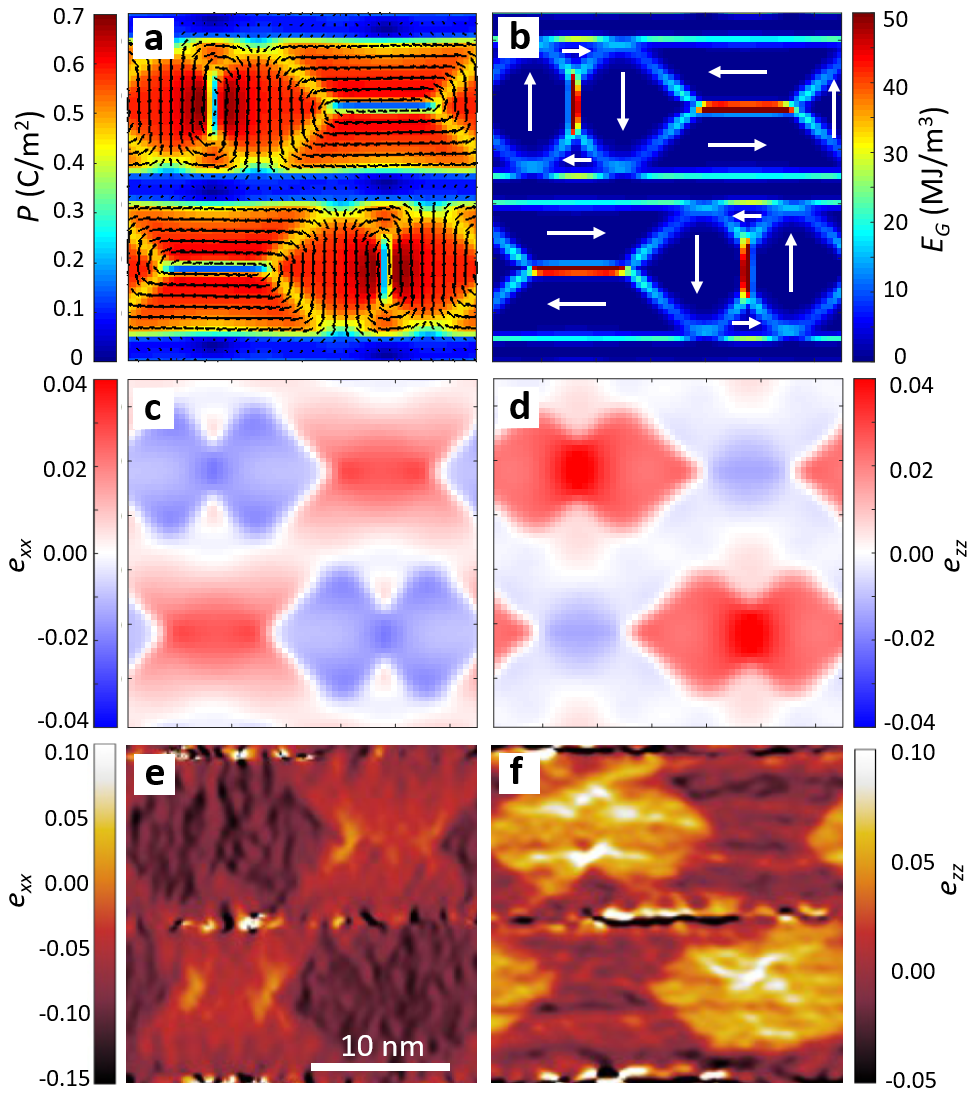
Figure:
Two-dimensional base motif of the ferroelectrically ordered PbTiO3–SrRuO3 superlattices as seen by
(a-d) phase-field simulations and (e,f) transmission electron microscopy:
(a) electric polarization showing ferroelectric domain structure in two PbTiO3 layers separated by SrRuO3 spacers
(b) gradient energy density coming from domain walls and boundaries between layers,
(c-f) in-plane (exx) and out-of-plane (ezz) strain components demonstrating correlations between ferroelectric PbTiO3 layers.
The arrows in (a,b) panels show direction of electric polarization forming characteristic flux-closure patterns.
[1] M. Hadjimichael, Y. Li, E. Zatterin, G. A. Chahine, M. Conroy, K. Moore, E. N. O’ Connell, P. Ondrejkovic, P. Marton, J. Hlinka, U. Bangert, S. Leake, and P. Zubko, Metal–ferroelectric supercrystals with periodically curved metallic layers, Nat. Mater. 20, 495 (2021).
(show less)
Existence conditions for ferroaxial materials
All 212 species of structural phase transitions with a macroscopic symmetry breaking were inspected with respect to the simultaneous occurrence of the ferroelastic, ferroelectric, and ferroaxial properties.
For each species, a matrix of representative equilibrium property tensors in both high-symmetry and low-symmetry phases, showing emergence of spontaneous components, were explicitly worked out [http://palata.fzu.cz/species/13x13axial]. Results can serve as a useful tool in search of fundamentally new material properties [J. Hlinka et al., Phys. Rev. Lett. 116, 177602 (2016)].
Figure: Dichromatic matrix of material property tensors for a symmetry-breaking structural phase transition from tetragonal to monoclinic phases, showing relations between tensor components of both phases and emergence of spontaneous components (red points).
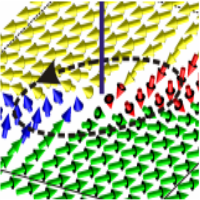
Ising lines: Natural topological defects within ferroelectric Bloch walls
Phase-field simulations demonstrate that the polarization order-parameter field in the Ginzburg-Landau-Devonshire model of rhombohedral ferroelectric BaTiO3 allows for an interesting linear defect, stable under simple periodic boundary conditions. This linear defect, here called the Ising line, can be described as an about 2-nm-thick intrinsic paraelectric nanorod acting as a highly mobile borderline between finite portions of Bloch-like domain walls of opposite helicity.
These Ising lines play the role of domain boundaries associated with the Ising-to-Bloch domain-wall phase transition. Therefore, the electric field parallel to the Ising line can be used to induce the Ising line motion, which mediates the switching of both polarization and chirality of the Bloch wall without changing the bulk domain polarization. Detailed description of this study can be found in the paper [ V. Stepkova, P. Marton, and J. Hlinka, Phys. Rev. B 92, 094106 (2015)]
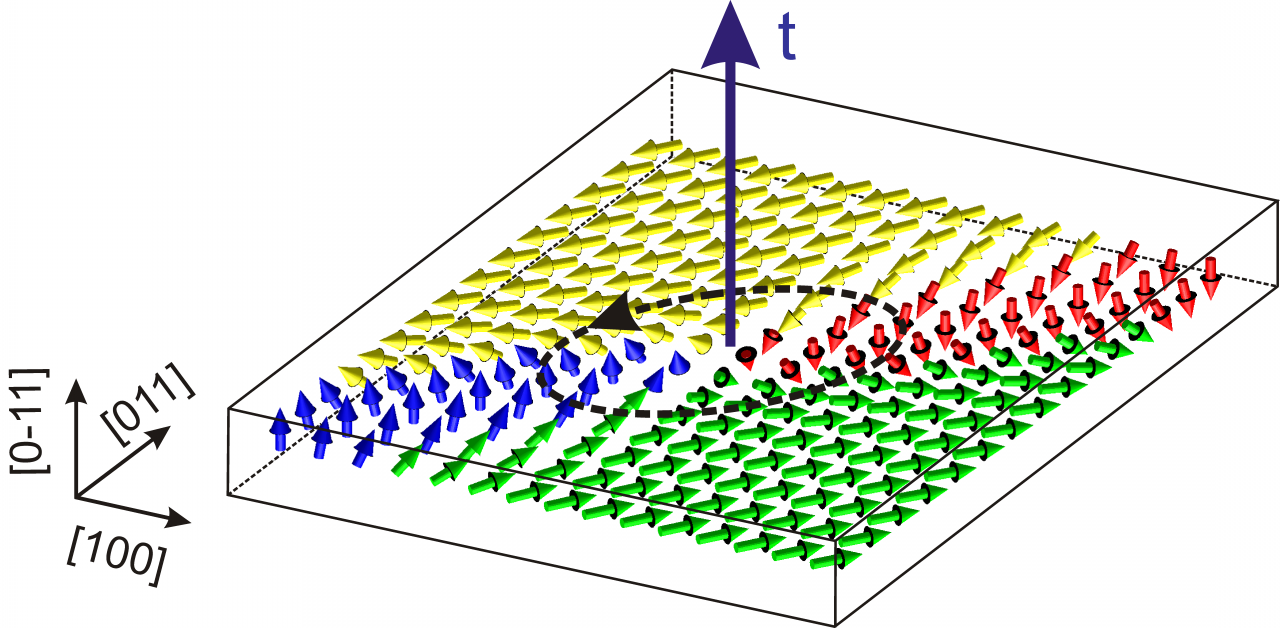
Figure: Ising line defect in rhombohedral BaTiO3. When circumventing the core of this defect following a closed path (dashed line) around its axis t, the polarization on this path rotates around the [-211] axis, which is perpendicular to t.
Phase transition in ferroelectric domain walls of BaTiO3
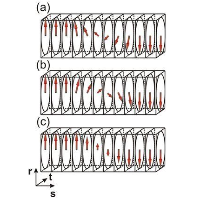
The seminal paper by Zhirnov (1958 Zh. Eksp. Teor. Fiz. 35 1175–80) explained why the structure of domain walls in ferroelectrics and ferromagnets is so different. We have recently realized that the antiparallel ferroelectric walls in rhombohedral ferroelectric BaTiO3 can be switched between the Ising-like state (typical for ferroelectrics) and a Bloch-like state (unusual for ferroelectric walls but typical for magnetic ones) [see Figure 1] by a compressive epitaxial stress.
Phase-field simulations using a Ginzburg–Landau–Devonshire model allows to explore this strain-induced phase transition within the domain wall in detail [Figure 2]. Strain-tunable chiral properties of ferroelectric Bloch walls promise a range of novel phenomena in epitaxial ferroelectric thin films. Results are published in JPCM [ V. Stepkova et al., J. Phys.: Condens. Matter 24, 212201 (2012)].
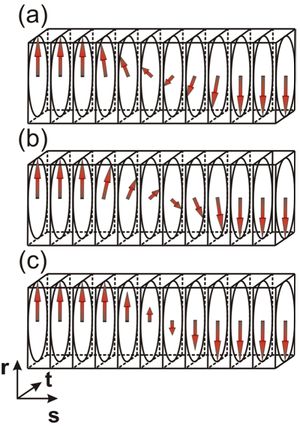
Figure 1: Variation of polarization P within Bloch- and Ising-type domain walls. The Bloch-type structure (a,b) conserves the magnitude of the local vectorial order parameter. This is typically encountered in ferromagnetism. In contrast, ferroelectric materials usually have large anisotropy and the magnitude of the polarization can be more easily adjusted. Therefore, antiparallel walls in ferroelectrics are known to correspond to the achiral Ising solution (c). We show here that in rhombohedral BaTiO3, both types of 180° domain walls can be stabilized.
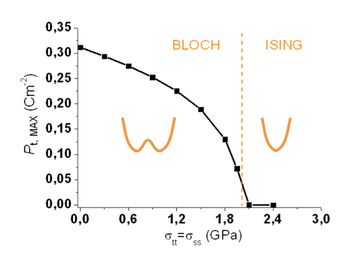
Figure 2: Chiral order parameter. The extremal value of the Pt polarization component in the core of the domain wall is plotted as a function of the epitaxial stress. This quantity can be taken as an order parameter of this chiral phase transition within the domain wall. For the wall under study, the phase transition is continuous and it can be associated with the Landau free-energy sketched in the figure.
Dielectric response of a phase transition in domain wall
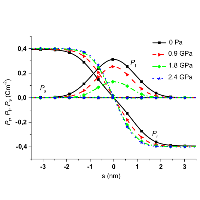
Computer simulations based on Ginzburg-Landau-Devonshire theory was used to study details of a phase-transition between Ising and Bloch type of a domain wall.
Such transition was predicted to appear for 180 degree domain wall in the rhombohedral ferroelectric phase of BaTiO3 close to 2GPa compressive stress [ V. Stepkova et al., J. Phys.: Condens. Matter 24, 212201 (2012)]. We confirm the hypothesis that the phase transition is of the first-order and predict corresponding divergent increase of the dielectric permittivity in the vicinity of the transition. In case of dense domain-wall pattern it can represent a substantial part of the dielectric response of the material [ P. Marton et al., Phase Transitions 86, 103 (2012)].
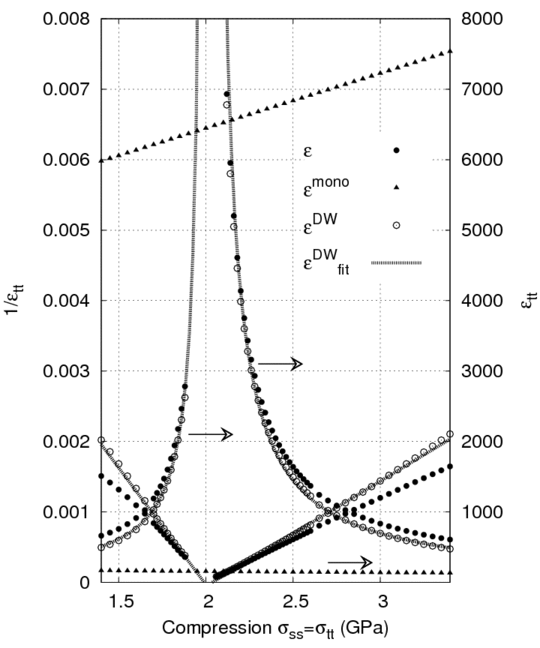
Figure 1: Dielectric permittivity in dependence on mechanical pressure in the vicinity of the transition from Ising (larger pressure) to Bloch-type of the domain wall.
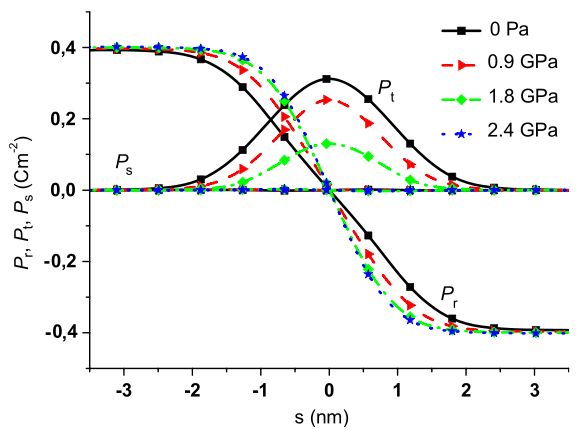
Figure 2: Bloch-to-Ising phase transition within a rhombohedral 180° domain wall.
Piezoelectric response of nanotwinned ferroelectric perovskites
Computer simulations based on Ginzburg-Landau-Devonshire theory has benn used to investigate piezoelectric properties of tetragonal BaTiO3 crystals. We have shown that piezoelectric response of twinned BaTiO3 increases with increasing density of 90-degree domain walls.
A considerable enhancement of piezoelectric coefficients is predicted below 50 nm. We have also shown that main contribution to the longitudinal piezoelectric coefficient comes from volume of domain, rather than from the domain wall region. Nevertheless, the experimentally reported impact of domain wall density is even stronger than in our simulations. Our most recent theoretical investigations [P. Marton et al, Physical Review B 81, 144125 (2010)] suggest that ferroelectric perovskites such as BaTiO3 most likely support also more exotic domain walls, resembling Bloch walls known from ferromagnetism. This kind of domain walls might account for additional enhancement of the electromechanical material response.
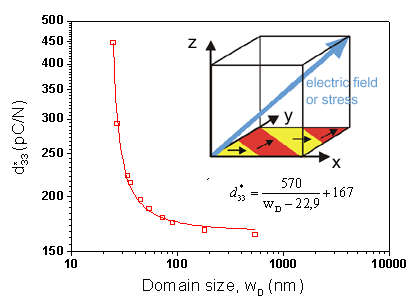
Figure 1: Dependence of the effective longitudinal piezoelectric coefficient on domain size calculated from the response of the ideal 2D laminar domain structure to weak uniaxial stresses applied along the [111] crystallographic direction. The inset shows the geometry of the initial 2D laminate domain structure assumed in the simulations.
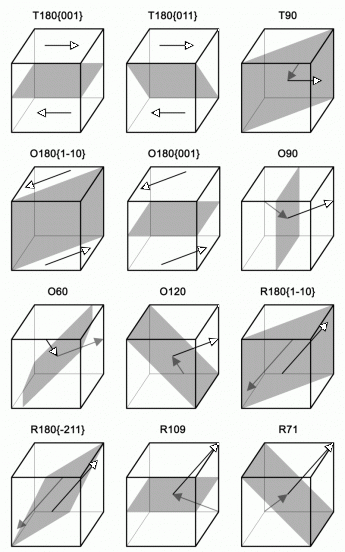
Figure 2: Set of mechanically compatible and electrically neutral domain walls in the three ferroelectric phases o f BaTiO3. Letter denominating the phase (T, O and R stay for tetragonal, orthorhombic and rhombohedral phase, resp.) is followed by an angle between the polarization in adjacent domains and in some cases also by the domain-wall normal.